993. 二叉树的堂兄弟节点

题目描述

在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。

如果二叉树的两个节点深度相同，但 父节点不同 ，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root ，以及树中两个不同节点的值 x 和 y 。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true 。否则，返回 false。

示例 1：

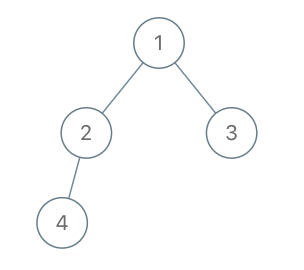
输入：root = [1,2,3,4], x = 4, y = 3
输出：false

示例 2：

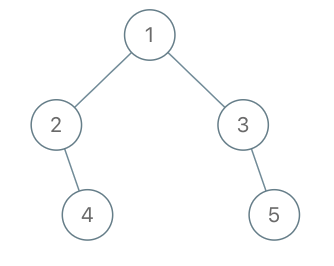
输入：root = [1,2,3,null,4,null,5], x = 5, y = 4
输出：true

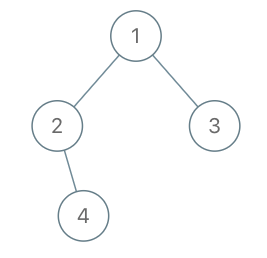
示例 3：

输入：root = [1,2,3,null,4], x = 2, y = 3
输出：false

提示：

二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。

解法

方法一：BFS

我们定义一个队列 $q$，队列中存储的是节点和其父节点。初始时，将根节点和空节点放入队列中。

每次从队列中取出一个节点，如果该节点的值为 $x$ 或 $y$，则记录该节点的父节点和深度。如果该节点的左右子节点不为空，则将左右子节点和该节点放入队列中。

当队列中所有节点都处理完毕后，如果 $x$ 和 $y$ 的深度相同且父节点不同，则返回 $true$，否则返回 $false$。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点数。

方法二：DFS

我们设计一个函数 $dfs(root, fa, d)$，表示从根节点 $root$ 出发，其父节点为 $fa$，深度为 $d$，进行深度优先搜索。

在函数中，我们首先判断当前节点是否为空，如果为空，则直接返回。如果当前节点的值为 $x$ 或 $y$，则记录该节点的父节点和深度。然后对当前节点的左右子节点分别调用函数 $dfs$，其中父节点为当前节点，深度为当前深度加 $1$。即 $dfs(root.left, root, d + 1)$ 和 $dfs(root.right, root, d + 1)$。

当整棵二叉树遍历完毕后，如果 $x$ 和 $y$ 的深度相同且父节点不同，则返回 $true$，否则返回 $false$。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点数。

Python3

BFS：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:
        q = deque([(root, None)])
        d = 0
        p1 = p2 = None
        d1 = d2 = 0
        while q:
            for _ in range(len(q)):
                node, fa = q.popleft()
                if node.val == x:
                    p1, d1 = fa, d
                if node.val == y:
                    p2, d2 = fa, d
                if node.left:
                    q.append((node.left, node))
                if node.right:
                    q.append((node.right, node))
            d += 1
        return p1 != p2 and d1 == d2

DFS：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:
        def dfs(root, fa, d):
            if root is None:
                return
            if root.val == x:
                t[0] = (fa, d)
            if root.val == y:
                t[1] = (fa, d)
            dfs(root.left, root, d + 1)
            dfs(root.right, root, d + 1)

        t = [None, None]
        dfs(root, None, 0)
        return t[0][0] != t[1][0] and t[0][1] == t[1][1]

Java

BFS：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isCousins(TreeNode root, int x, int y) {
        TreeNode p1 = null, p2 = null;
        int d1 = 0, d2 = 0;
        Deque<TreeNode[]> q = new ArrayDeque<>();
        q.offer(new TreeNode[] {root, null});
        int d = 0;
        while (!q.isEmpty()) {
            for (int n = q.size(); n > 0; --n) {
                var p = q.poll();
                TreeNode node = p[0], fa = p[1];
                if (node.val == x) {
                    p1 = fa;
                    d1 = d;
                }
                if (node.val == y) {
                    p2 = fa;
                    d2 = d;
                }
                if (node.left != null) {
                    q.offer(new TreeNode[] {node.left, node});
                }
                if (node.right != null) {
                    q.offer(new TreeNode[] {node.right, node});
                }
            }
            ++d;
        }
        return p1 != p2 && d1 == d2;
    }
}

DFS：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int x, y;
    private TreeNode p1, p2;
    private int d1, d2;

    public boolean isCousins(TreeNode root, int x, int y) {
        this.x = x;
        this.y = y;
        dfs(root, null, 0);
        return p1 != p2 && d1 == d2;
    }

    private void dfs(TreeNode root, TreeNode p, int d) {
        if (root == null) {
            return;
        }
        if (root.val == x) {
            p1 = p;
            d1 = d;
        }
        if (root.val == y) {
            p2 = p;
            d2 = d;
        }
        dfs(root.left, root, d + 1);
        dfs(root.right, root, d + 1);
    }
}

C++

BFS：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isCousins(TreeNode* root, int x, int y) {
        TreeNode* p1 = nullptr;
        TreeNode* p2 = nullptr;
        int d1 = 0, d2 = 0;
        queue<pair<TreeNode*, TreeNode*>> q;
        q.emplace(root, nullptr);
        int d = 0;
        while (!q.empty()) {
            for (int n = q.size(); n; --n) {
                auto [node, fa] = q.front();
                q.pop();
                if (node->val == x) {
                    p1 = fa;
                    d1 = d;
                }
                if (node->val == y) {
                    p2 = fa;
                    d2 = d;
                }
                if (node->left) {
                    q.emplace(node->left, node);
                }
                if (node->right) {
                    q.emplace(node->right, node);
                }
            }
            ++d;
        }
        return p1 != p2 && d1 == d2;
    }
};

DFS：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isCousins(TreeNode* root, int x, int y) {
        TreeNode *p1, *p2;
        int d1, d2;
        function<void(TreeNode*, TreeNode*, int)> dfs = [&](TreeNode* root, TreeNode* fa, int d) {
            if (!root) {
                return;
            }
            if (root->val == x) {
                p1 = fa;
                d1 = d;
            }
            if (root->val == y) {
                p2 = fa;
                d2 = d;
            }
            dfs(root->left, root, d + 1);
            dfs(root->right, root, d + 1);
        };
        dfs(root, nullptr, 0);
        return p1 != p2 && d1 == d2;
    }
};

Go

BFS：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isCousins(root *TreeNode, x int, y int) bool {
	type pair struct{ node, fa *TreeNode }
	q := []pair{pair{root, nil}}
	var p1, p2 *TreeNode
	var d, d1, d2 int
	for len(q) > 0 {
		for n := len(q); n > 0; n-- {
			p := q[0]
			q = q[1:]
			node, fa := p.node, p.fa
			if node.Val == x {
				p1, d1 = fa, d
			}
			if node.Val == y {
				p2, d2 = fa, d
			}
			if node.Left != nil {
				q = append(q, pair{node.Left, node})
			}
			if node.Right != nil {
				q = append(q, pair{node.Right, node})
			}
		}
		d++
	}
	return p1 != p2 && d1 == d2
}

DFS：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isCousins(root *TreeNode, x int, y int) bool {
	var p1, p2 *TreeNode
	var d1, d2 int
	var dfs func(*TreeNode, *TreeNode, int)
	dfs = func(root *TreeNode, fa *TreeNode, d int) {
		if root == nil {
			return
		}
		if root.Val == x {
			p1, d1 = fa, d
		}
		if root.Val == y {
			p2, d2 = fa, d
		}
		dfs(root.Left, root, d+1)
		dfs(root.Right, root, d+1)
	}
	dfs(root, nil, 0)
	return p1 != p2 && d1 == d2
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

993. 二叉树的堂兄弟节点

题目描述

解法

Python3

Java

C++

Go

...

Files

README.md

Latest commit

History

README.md

File metadata and controls

993. 二叉树的堂兄弟节点

题目描述

解法

Python3

Java

C++

Go

...