Skip to content

Latest commit

 

History

History
296 lines (255 loc) · 9 KB

README.md

File metadata and controls

296 lines (255 loc) · 9 KB

971. 翻转二叉树以匹配先序遍历

English Version

题目描述

给你一棵二叉树的根节点 root ，树中有 n 个节点，每个节点都有一个不同于其他节点且处于 1 到 n 之间的值。

另给你一个由 n 个值组成的行程序列 voyage ，表示 预期 的二叉树 先序遍历 结果。

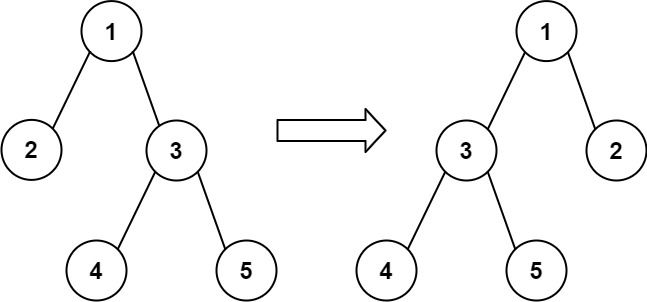
通过交换节点的左右子树，可以 翻转 该二叉树中的任意节点。例，翻转节点 1 的效果如下：

请翻转 最少 的树中节点，使二叉树的 先序遍历 与预期的遍历行程 voyage 相匹配 。 

如果可以，则返回 翻转的 所有节点的值的列表。你可以按任何顺序返回答案。如果不能，则返回列表 [-1]。

 

示例 1：

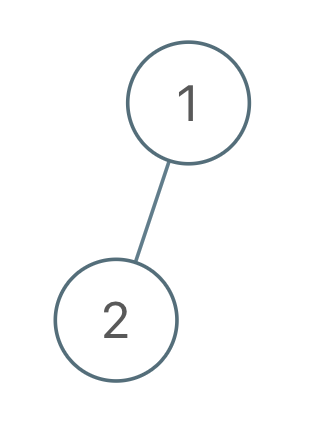
输入：root = [1,2], voyage = [2,1]
输出：[-1]
解释：翻转节点无法令先序遍历匹配预期行程。

示例 2：

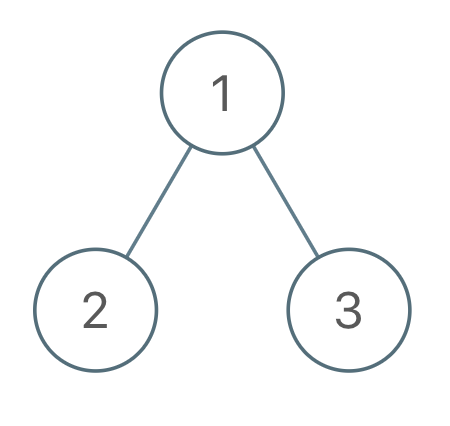
输入：root = [1,2,3], voyage = [1,3,2]
输出：[1]
解释：交换节点 2 和 3 来翻转节点 1 ，先序遍历可以匹配预期行程。

示例 3：

输入：root = [1,2,3], voyage = [1,2,3]
输出：[]
解释：先序遍历已经匹配预期行程，所以不需要翻转节点。

 

提示：

  • 树中的节点数目为 n
  • n == voyage.length
  • 1 <= n <= 100
  • 1 <= Node.val, voyage[i] <= n
  • 树中的所有值 互不相同
  • voyage 中的所有值 互不相同

解法

方法一：DFS

我们可以通过深度优先搜索的方式遍历整棵树，用一个下标 $i$ 记录当前遍历到的节点在数组 $voyage$ 中的下标，如果当前遍历到的节点的值不等于 $voyage[i]$，那么说明翻转后无法匹配，我们标记 $ok$ 为 false，并直接返回。否则，我们将 $i$ 的值加 $1$，然后判断当前节点是否有左子节点，如果没有，或者左子节点的值等于 $voyage[i]$，那么我们递归遍历当前的左右子节点；否则，我们需要翻转当前节点，然后再递归遍历当前的右子节点和左子节点。

搜索结束后，如果 $ok$ 为 true，那么说明翻转后可以匹配，我们返回答案数组 $ans$，否则返回 $[-1]$。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是树中的节点数目。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def flipMatchVoyage(self, root: Optional[TreeNode], voyage: List[int]) -> List[int]:
        def dfs(root):
            nonlocal i, ok
            if root is None or not ok:
                return
            if root.val != voyage[i]:
                ok = False
                return
            i += 1
            if root.left is None or root.left.val == voyage[i]:
                dfs(root.left)
                dfs(root.right)
            else:
                ans.append(root.val)
                dfs(root.right)
                dfs(root.left)

        ans = []
        i = 0
        ok = True
        dfs(root)
        return ans if ok else [-1]

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int i;
    private boolean ok;
    private int[] voyage;
    private List<Integer> ans = new ArrayList<>();

    public List<Integer> flipMatchVoyage(TreeNode root, int[] voyage) {
        this.voyage = voyage;
        ok = true;
        dfs(root);
        return ok ? ans : List.of(-1);
    }

    private void dfs(TreeNode root) {
        if (root == null || !ok) {
            return;
        }
        if (root.val != voyage[i]) {
            ok = false;
            return;
        }
        ++i;
        if (root.left == null || root.left.val == voyage[i]) {
            dfs(root.left);
            dfs(root.right);
        } else {
            ans.add(root.val);
            dfs(root.right);
            dfs(root.left);
        }
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> flipMatchVoyage(TreeNode* root, vector<int>& voyage) {
        bool ok = true;
        int i = 0;
        vector<int> ans;
        function<void(TreeNode*)> dfs = [&](TreeNode* root) {
            if (!root || !ok) {
                return;
            }
            if (root->val != voyage[i]) {
                ok = false;
                return;
            }
            ++i;
            if (!root->left || root->left->val == voyage[i]) {
                dfs(root->left);
                dfs(root->right);
            } else {
                ans.push_back(root->val);
                dfs(root->right);
                dfs(root->left);
            }
        };
        dfs(root);
        return ok ? ans : vector<int>{-1};
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func flipMatchVoyage(root *TreeNode, voyage []int) []int {
	i := 0
	ok := true
	ans := []int{}
	var dfs func(*TreeNode)
	dfs = func(root *TreeNode) {
		if root == nil || !ok {
			return
		}
		if root.Val != voyage[i] {
			ok = false
			return
		}
		i++
		if root.Left == nil || root.Left.Val == voyage[i] {
			dfs(root.Left)
			dfs(root.Right)
		} else {
			ans = append(ans, root.Val)
			dfs(root.Right)
			dfs(root.Left)
		}
	}
	dfs(root)
	if !ok {
		return []int{-1}
	}
	return ans
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function flipMatchVoyage(root: TreeNode | null, voyage: number[]): number[] {
    let ok = true;
    let i = 0;
    const ans: number[] = [];
    const dfs = (root: TreeNode | null): void => {
        if (!root || !ok) {
            return;
        }
        if (root.val !== voyage[i++]) {
            ok = false;
            return;
        }
        if (!root.left || root.left.val === voyage[i]) {
            dfs(root.left);
            dfs(root.right);
        } else {
            ans.push(root.val);
            dfs(root.right);
            dfs(root.left);
        }
    };
    dfs(root);
    return ok ? ans : [-1];
}

...