Skip to content

Latest commit

 

History

History
204 lines (162 loc) · 5.04 KB

README.md

File metadata and controls

204 lines (162 loc) · 5.04 KB

935. 骑士拨号器

English Version

题目描述

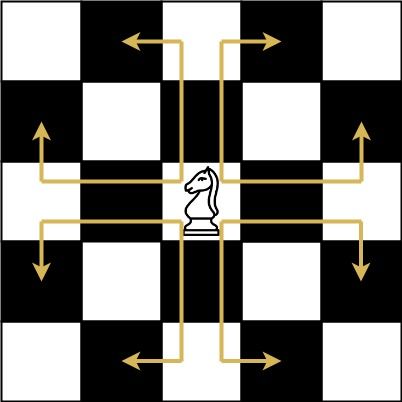
象棋骑士有一个独特的移动方式，它可以垂直移动两个方格，水平移动一个方格，或者水平移动两个方格，垂直移动一个方格(两者都形成一个 L 的形状)。

象棋骑士可能的移动方式如下图所示:

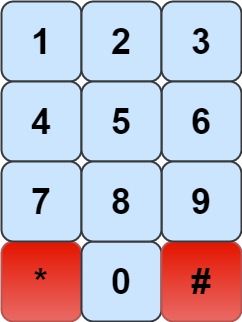
我们有一个象棋骑士和一个电话垫，如下所示，骑士只能站在一个数字单元格上(即蓝色单元格)。

给定一个整数 n，返回我们可以拨多少个长度为 n 的不同电话号码。

你可以将骑士放置在任何数字单元格上，然后你应该执行 n - 1 次移动来获得长度为 n 的号码。所有的跳跃应该是有效的骑士跳跃。

因为答案可能很大，所以输出答案模 109 + 7.

 

示例 1：

输入：n = 1
输出：10
解释：我们需要拨一个长度为1的数字，所以把骑士放在10个单元格中的任何一个数字单元格上都能满足条件。

示例 2：

输入：n = 2
输出：20
解释：我们可以拨打的所有有效号码为[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

示例 3：

输入：n = 3131
输出：136006598
解释：注意取模

 

提示：

  • 1 <= n <= 5000

解法

方法一：递推

Python3

class Solution:
    def knightDialer(self, n: int) -> int:
        if n == 1:
            return 10
        f = [1] * 10
        for _ in range(n - 1):
            t = [0] * 10
            t[0] = f[4] + f[6]
            t[1] = f[6] + f[8]
            t[2] = f[7] + f[9]
            t[3] = f[4] + f[8]
            t[4] = f[0] + f[3] + f[9]
            t[6] = f[0] + f[1] + f[7]
            t[7] = f[2] + f[6]
            t[8] = f[1] + f[3]
            t[9] = f[2] + f[4]
            f = t
        return sum(t) % (10**9 + 7)

Java

class Solution {
    private static final int MOD = (int) 1e9 + 7;

    public int knightDialer(int n) {
        if (n == 1) {
            return 10;
        }
        long[] f = new long[10];
        Arrays.fill(f, 1);
        while (--n > 0) {
            long[] t = new long[10];
            t[0] = f[4] + f[6];
            t[1] = f[6] + f[8];
            t[2] = f[7] + f[9];
            t[3] = f[4] + f[8];
            t[4] = f[0] + f[3] + f[9];
            t[6] = f[0] + f[1] + f[7];
            t[7] = f[2] + f[6];
            t[8] = f[1] + f[3];
            t[9] = f[2] + f[4];
            for (int i = 0; i < 10; ++i) {
                f[i] = t[i] % MOD;
            }
        }
        long ans = 0;
        for (long v : f) {
            ans = (ans + v) % MOD;
        }
        return (int) ans;
    }
}

C++

using ll = long long;

class Solution {
public:
    int knightDialer(int n) {
        if (n == 1) return 10;
        int mod = 1e9 + 7;
        vector<ll> f(10, 1ll);
        while (--n) {
            vector<ll> t(10);
            t[0] = f[4] + f[6];
            t[1] = f[6] + f[8];
            t[2] = f[7] + f[9];
            t[3] = f[4] + f[8];
            t[4] = f[0] + f[3] + f[9];
            t[6] = f[0] + f[1] + f[7];
            t[7] = f[2] + f[6];
            t[8] = f[1] + f[3];
            t[9] = f[2] + f[4];
            for (int i = 0; i < 10; ++i) f[i] = t[i] % mod;
        }
        ll ans = accumulate(f.begin(), f.end(), 0ll);
        return (int) (ans % mod);
    }
};

Go

func knightDialer(n int) int {
	if n == 1 {
		return 10
	}
	f := make([]int, 10)
	for i := range f {
		f[i] = 1
	}
	mod := int(1e9) + 7
	for i := 1; i < n; i++ {
		t := make([]int, 10)
		t[0] = f[4] + f[6]
		t[1] = f[6] + f[8]
		t[2] = f[7] + f[9]
		t[3] = f[4] + f[8]
		t[4] = f[0] + f[3] + f[9]
		t[6] = f[0] + f[1] + f[7]
		t[7] = f[2] + f[6]
		t[8] = f[1] + f[3]
		t[9] = f[2] + f[4]
		for j, v := range t {
			f[j] = v % mod
		}
	}
	ans := 0
	for _, v := range f {
		ans = (ans + v) % mod
	}
	return ans
}

...