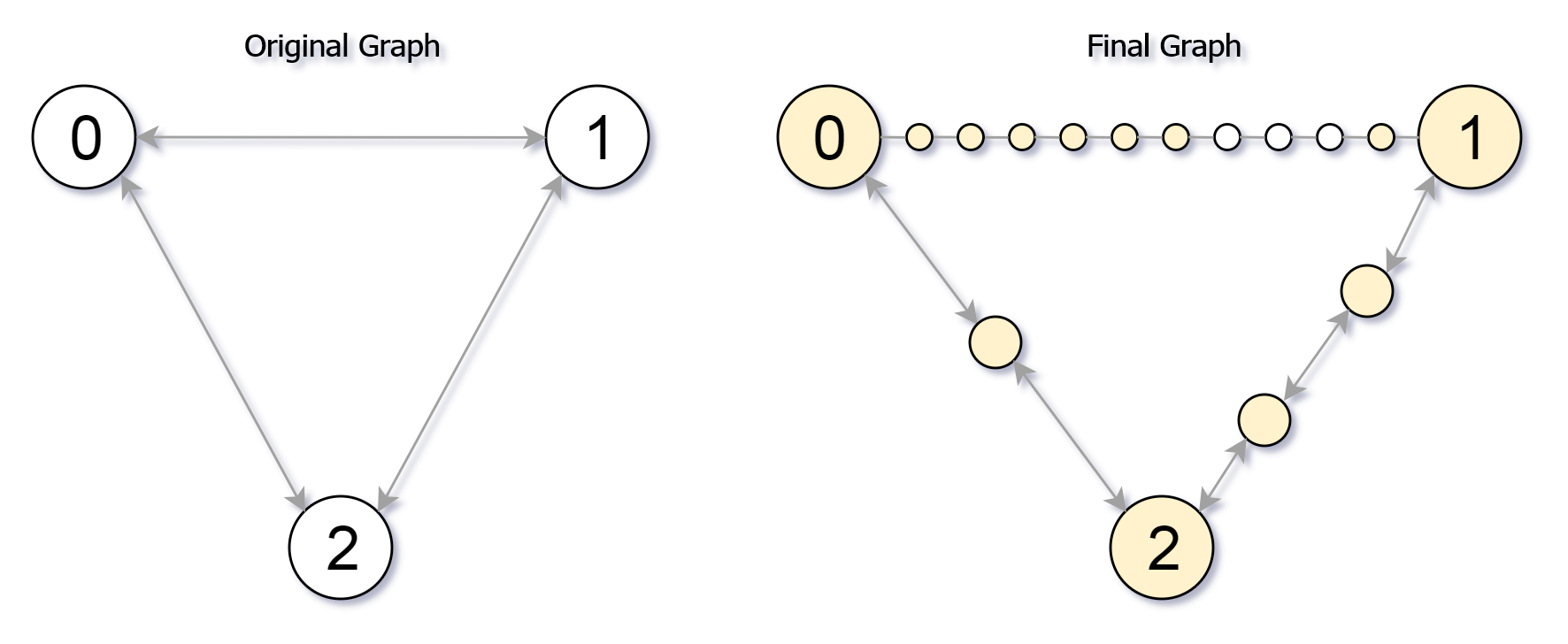
给你一个无向图(原始图),图中有 n 个节点,编号从 0 到 n - 1 。你决定将图中的每条边 细分 为一条节点链,每条边之间的新节点数各不相同。
图用由边组成的二维数组 edges 表示,其中 edges[i] = [ui, vi, cnti] 表示原始图中节点 ui 和 vi 之间存在一条边,cnti 是将边 细分 后的新节点总数。注意,cnti == 0 表示边不可细分。
要 细分 边 [ui, vi] ,需要将其替换为 (cnti + 1) 条新边,和 cnti 个新节点。新节点为 x1, x2, ..., xcnti ,新边为 [ui, x1], [x1, x2], [x2, x3], ..., [xcnti-1, xcnti], [xcnti, vi] 。
现在得到一个 新的细分图 ,请你计算从节点 0 出发,可以到达多少个节点?如果节点间距离是 maxMoves 或更少,则视为 可以到达 。
给你原始图和 maxMoves ,返回 新的细分图中从节点 0 出发 可到达的节点数 。
示例 1:
输入:edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3 输出:13 解释:边的细分情况如上图所示。 可以到达的节点已经用黄色标注出来。
示例 2:
输入:edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], maxMoves = 10, n = 4 输出:23
示例 3:
输入:edges = [[1,2,4],[1,4,5],[1,3,1],[2,3,4],[3,4,5]], maxMoves = 17, n = 5 输出:1 解释:节点 0 与图的其余部分没有连通,所以只有节点 0 可以到达。
提示:
0 <= edges.length <= min(n * (n - 1) / 2, 104)edges[i].length == 30 <= ui < vi < n- 图中 不存在平行边
0 <= cnti <= 1040 <= maxMoves <= 1091 <= n <= 3000
方法一:Dijkstra 算法
这道题本质是求从节点
根据题目描述,节点
我们举个简单的例子,以下节点
1 -- o -- o -- o -- 2
因此,我们可以将原图中两点之间新节点的个数
接下来,我们使用 Dijkstra 算法求出从节点
然后,我们遍历数组
我们可以发现,如果我们能在
因此,我们再遍历所有的边,统计其中能到达的新节点个数,累加到答案中即可。
时间复杂度
class Solution:
def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:
g = defaultdict(list)
for u, v, cnt in edges:
g[u].append((v, cnt + 1))
g[v].append((u, cnt + 1))
q = [(0, 0)]
dist = [0] + [inf] * n
while q:
d, u = heappop(q)
for v, cnt in g[u]:
if (t := d + cnt) < dist[v]:
dist[v] = t
q.append((t, v))
ans = sum(d <= maxMoves for d in dist)
for u, v, cnt in edges:
a = min(cnt, max(0, maxMoves - dist[u]))
b = min(cnt, max(0, maxMoves - dist[v]))
ans += min(cnt, a + b)
return ansclass Solution {
public int reachableNodes(int[][] edges, int maxMoves, int n) {
List<int[]>[] g = new List[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int u = e[0], v = e[1], cnt = e[2] + 1;
g[u].add(new int[] {v, cnt});
g[v].add(new int[] {u, cnt});
}
int[] dist = new int[n];
Arrays.fill(dist, 1 << 30);
PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]);
q.offer(new int[] {0, 0});
dist[0] = 0;
while (!q.isEmpty()) {
var p = q.poll();
int d = p[0], u = p[1];
for (var nxt : g[u]) {
int v = nxt[0], cnt = nxt[1];
if (d + cnt < dist[v]) {
dist[v] = d + cnt;
q.offer(new int[] {dist[v], v});
}
}
}
int ans = 0;
for (int d : dist) {
if (d <= maxMoves) {
++ans;
}
}
for (var e : edges) {
int u = e[0], v = e[1], cnt = e[2];
int a = Math.min(cnt, Math.max(0, maxMoves - dist[u]));
int b = Math.min(cnt, Math.max(0, maxMoves - dist[v]));
ans += Math.min(cnt, a + b);
}
return ans;
}
}class Solution {
public:
int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
using pii = pair<int, int>;
vector<vector<pii>> g(n);
for (auto& e : edges) {
int u = e[0], v = e[1], cnt = e[2] + 1;
g[u].emplace_back(v, cnt);
g[v].emplace_back(u, cnt);
}
priority_queue<pii, vector<pii>, greater<pii>> q;
q.emplace(0, 0);
int dist[n];
memset(dist, 0x3f, sizeof dist);
dist[0] = 0;
while (!q.empty()) {
auto [d, u] = q.top();
q.pop();
for (auto& [v, cnt] : g[u]) {
if (d + cnt < dist[v]) {
dist[v] = d + cnt;
q.emplace(dist[v], v);
}
}
}
int ans = 0;
for (int& d : dist) ans += d <= maxMoves;
for (auto& e : edges) {
int u = e[0], v = e[1], cnt = e[2];
int a = min(cnt, max(0, maxMoves - dist[u]));
int b = min(cnt, max(0, maxMoves - dist[v]));
ans += min(cnt, a + b);
}
return ans;
}
};func reachableNodes(edges [][]int, maxMoves int, n int) (ans int) {
g := make([][]pair, n)
for _, e := range edges {
u, v, cnt := e[0], e[1], e[2]+1
g[u] = append(g[u], pair{cnt, v})
g[v] = append(g[v], pair{cnt, u})
}
dist := make([]int, n)
for i := range dist {
dist[i] = 1 << 30
}
dist[0] = 0
q := hp{{0, 0}}
for len(q) > 0 {
p := heap.Pop(&q).(pair)
d, u := p.v, p.i
for _, nxt := range g[u] {
v, cnt := nxt.i, nxt.v
if t := d + cnt; t < dist[v] {
dist[v] = t
heap.Push(&q, pair{t, v})
}
}
}
for _, d := range dist {
if d <= maxMoves {
ans++
}
}
for _, e := range edges {
u, v, cnt := e[0], e[1], e[2]
a := min(cnt, max(0, maxMoves-dist[u]))
b := min(cnt, max(0, maxMoves-dist[v]))
ans += min(cnt, a+b)
}
return
}
type pair struct{ v, i int }
type hp []pair
func (h hp) Len() int { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].v < h[j].v }
func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v interface{}) { *h = append(*h, v.(pair)) }
func (h *hp) Pop() interface{} { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}