Skip to content

Latest commit

 

History

History
135 lines (98 loc) · 4.88 KB

0141.环形链表.md

File metadata and controls

135 lines (98 loc) · 4.88 KB
Raw

欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

141. 环形链表

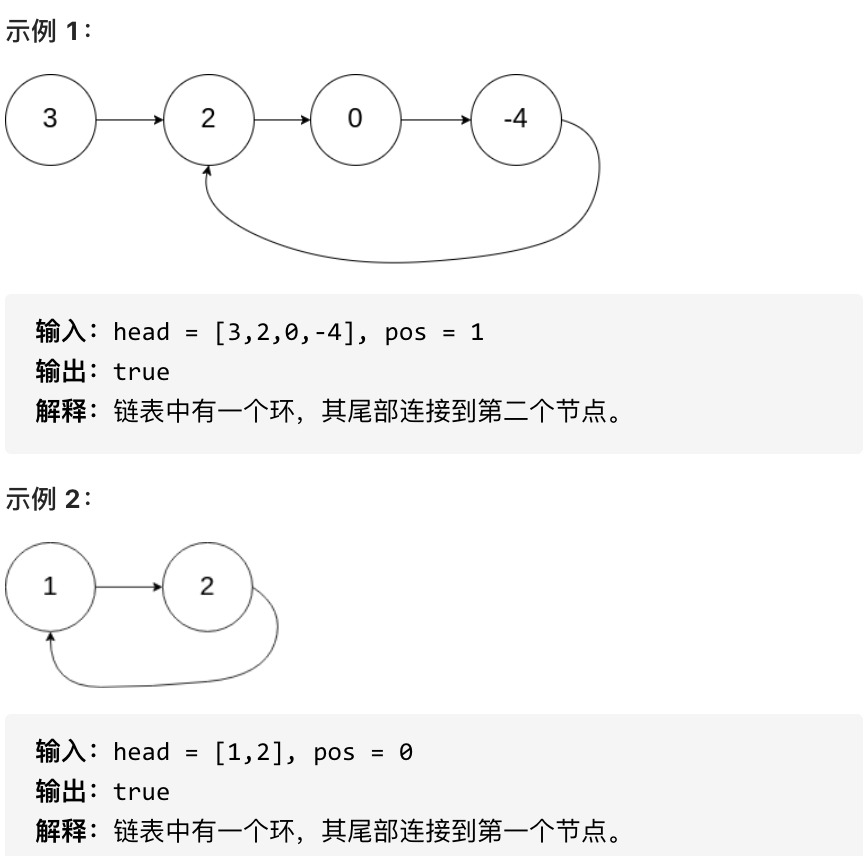
给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。 否则，返回 false 。

思路

可以使用快慢指针法， 分别定义 fast 和 slow指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇 ，说明这个链表有环。

为什么fast 走两个节点，slow走一个节点，有环的话，一定会在环内相遇呢，而不是永远的错开呢？

首先第一点： fast指针一定先进入环中，如果fast 指针和slow指针相遇的话，一定是在环中相遇，这是毋庸置疑的。

那么来看一下，为什么fast指针和slow指针一定会相遇呢？

可以画一个环，然后让 fast指针在任意一个节点开始追赶slow指针。

会发现最终都是这种情况， 如下图：

fast和slow各自再走一步， fast和slow就相遇了

这是因为fast是走两步，slow是走一步，其实相对于slow来说，fast是一个节点一个节点的靠近slow的，所以fast一定可以和slow重合。

动画如下：

141.环形链表

C++代码如下

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != NULL && fast->next != NULL) {
            slow = slow->next;
            fast = fast->next->next;
            // 快慢指针相遇，说明有环
            if (slow == fast) return true;
        }
        return false;
    }
};

扩展

做完这道题目，可以在做做142.环形链表II，不仅仅要找环，还要找环的入口。

142.环形链表II题解：链表：环找到了，那入口呢？

其他语言版本

Java

public class Solution {
    public boolean hasCycle(ListNode head) {
		ListNode fast = head;
		ListNode slow = head;
		// 空链表、单节点链表一定不会有环
		while (fast != null && fast.next != null) {
			fast = fast.next.next; // 快指针，一次移动两步
			slow = slow.next;      // 慢指针，一次移动一步
			if (fast == slow) {   // 快慢指针相遇，表明有环
				return true;
			}
		}
		return false; // 正常走到链表末尾，表明没有环
    }
}

Python

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        if not head: return False
        slow, fast = head, head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
            if fast == slow:
                return True
        return False

Go



JavaScript


var hasCycle = function(head) {
    let fast = head;
    let slow = head;
    // 空链表、单节点链表一定不会有环
    while(fast != null && fast.next != null){
        fast = fast.next.next; // 快指针，一次移动两步
        slow = slow.next; // 慢指针，一次移动一步
        if(fast === slow) return true; // 快慢指针相遇，表明有环
    }
    return false; // 正常走到链表末尾，表明没有环
};