-
Notifications
You must be signed in to change notification settings - Fork 65
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
find_fisher_stats doesn't calculate fisher k or mean vector correctly for groups of poles which cross the dip=90 line #39
Comments
|
Ok, I figured out a better solution to figure out the mean vector mean_vec. This uses the scatter matrix approach from Directional Statistics (Jupp and Mardia, 2000, pp.165). |
|
I'll figure out how to make a pull request, but in the meantime here's a working update to the fisher_stats function that fixes the issues with mean orientation and kappa. |
This was referenced Mar 24, 2021
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
Hi Joe,
The find_fisher_stats, fisher_stats, and mean_vector functions don't seem to be calculating Fisher k (kappa) or the mean vector of a group of poles correctly where the group of poles includes orientations which cross a dip=90°.
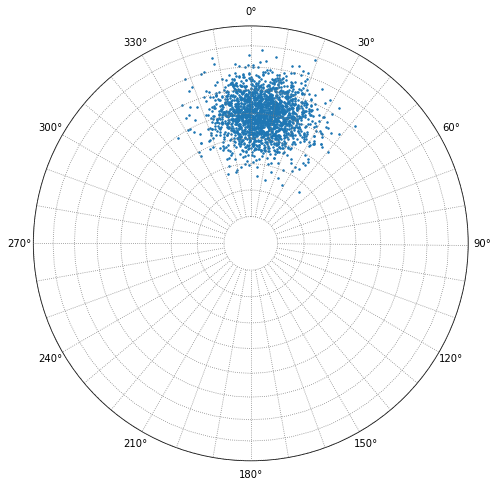
For example, the Fisher K and mean vector for this group of poles is correct. Calculated mean dip is 50°, Fisher K is 50.
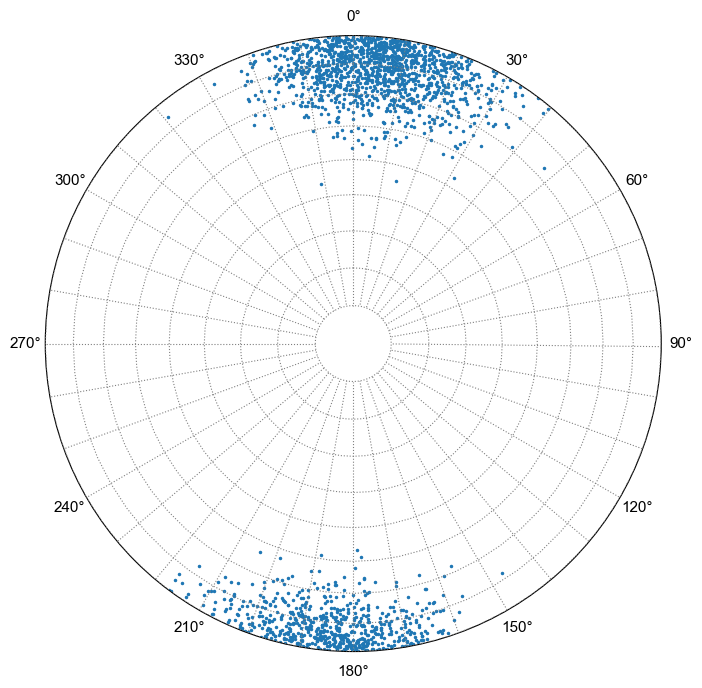
But, for this example the distribution has an actual Fisher k value of 25 and a mean dip of 85°, but the calculated kappa is 1.6 and the calculated mean dip is 62°.
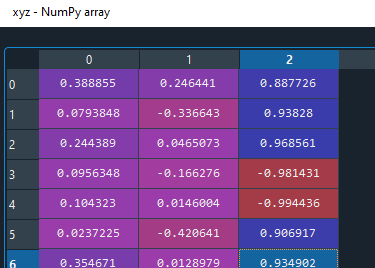
I think the issue is the lines of code where you take the mean of the vectors.
xyz = np.vstack(xyz).T
mean_vec = xyz.mean(axis=0)
When the largest eigenvalue flips direction, just taking the mean gives you a bad result.
As a hack/workaround, I think you can do something like flip the normals so they all point in the same direction:
le = np.argmax(np.max(np.abs(xyz), axis=0)) # largest eigenvalue is the one we should normalize the others by
cond = xyz[:,le]<0
xyz = np.where(cond[:,None],xyz*-1,xyz)
But I bet you can come up with a better solution. This library is awesome, thanks for all your work on it!
The text was updated successfully, but these errors were encountered: