-
Notifications
You must be signed in to change notification settings - Fork 3
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Feature Request: Binomial Coefficient Entropy Coding for Inverted Index Postings #1
Comments
|
Hi there and thank you very much for your interest! The issue seems that you can only decode sequentially and, actually, backward. Each decoding operation is essentially a search for the proper binomial coefficient (as you pointed out, this could be probably sped up using a lookup table). It would need some work and extensive testing to make this proposal useful as a coding option for inverted lists. Again, thank you for your insightful comments! |
|
Thank you for this response! Forgive me for my ignorance. What is the preferred method for compressing inverted lists? Do people typically use roaring bitmaps or is there another method? Thank you for your time. |
|
Well, you referred to our survey paper on the subject, so give it a read to find the answer :) Also, your proposal is reminiscent of the so-called "RRR" encoding. |
|
Thank you so much for this! I appreciate your time. Please let me know if you would like to collaborate on this. Perhaps, you could open a repo and I could share these fast implementations. You don't have to do this, but I would love to contribute if you do. You can email me at [email protected] if you want to talk about this. Thank you! |
Summary
This is a proposal for encoding inverted index integer sequences using a number system based on binomial coefficients.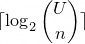
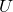 is largest number in the list and
is largest number in the list and 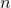 is the number of elements in the list.
is the number of elements in the list.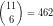 and
and
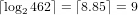 .
.
This number system is chosen because the minimum number of bits needed to encode a list of strictly increasing integers
is given by the equation
where
For example to encode the sequence 1,2,3,4,10,11 we need at least 9 bits:
Binary interpolative coding, one of the best methods for inverted list compression takes at least 20 bits to represent the example sequence. You can confirm this here.
However, if we represent the same sequence as a sum of binomial coefficients, it takes 10 bits to encode the list, and an extra 3 bits to store the length of the list. The total is 13 bits. You can confirm this here.
Motivation
Compression is a solved problem. The best compressors work by changing radixes, or number bases to find the most concise representation of data.
For instance, arithmetic coding is a generalized change of radix for coding
at the information theoretic entropy bound. This bound is a measure of redundancy - how many duplicates are in your data. Strictly increasing integer sequences have no duplicates, therefore, cannot be compressed
according to the information theoretic bound. This means huffman coding and arithmetic coding methods are inefficient with non-repetitive integer sequences.
This rfc proposes the use of the combinatorial number system to encode inverted index integer sequences at the combinatorial information theoretic entropy bound.
Just like arithmetic coding, this change in number systems allows us to encode integer sequences with the least number of bits.
I am a Math major in my junior year and if this RFC succeeds I would love to take a gap year and work on this library full time. The library
has sample code for converting between binary and the combinatorial number system using a greedy algorithm, or by generating a lookup table.
Technical design
Overview of Combinatorial Number System
Any natural number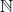 can be uniquely written as a sum of binomial coefficients
can be uniquely written as a sum of binomial coefficients
using this greedy algorithm.
Example: Find the combinatorial representation of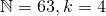
To reverse the process, sum your list of binomial coefficients
Comparison to Binary Interpolative Coding
In the example above, it can be seen that the sequence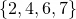
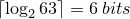 using the combinatorial number system with an extra 3 bits to store the length of the sequence. This is a total of 9 bits to encode this sequence.
using the combinatorial number system with an extra 3 bits to store the length of the sequence. This is a total of 9 bits to encode this sequence.
can be encoded in
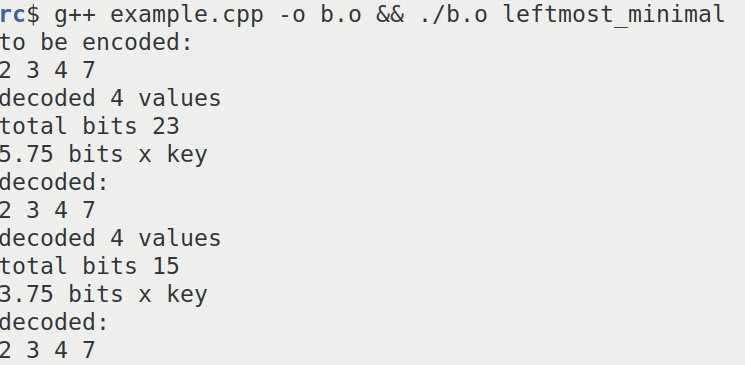
Using this library it can be confirmed that binary interpolative coding takes between 15 to 23 bits to encode the same sequence.
This is a screenshot of the result of binary interpolative coding.
The combinatorial number systems always encodes integer sequences at the entropy limit.
The text was updated successfully, but these errors were encountered: