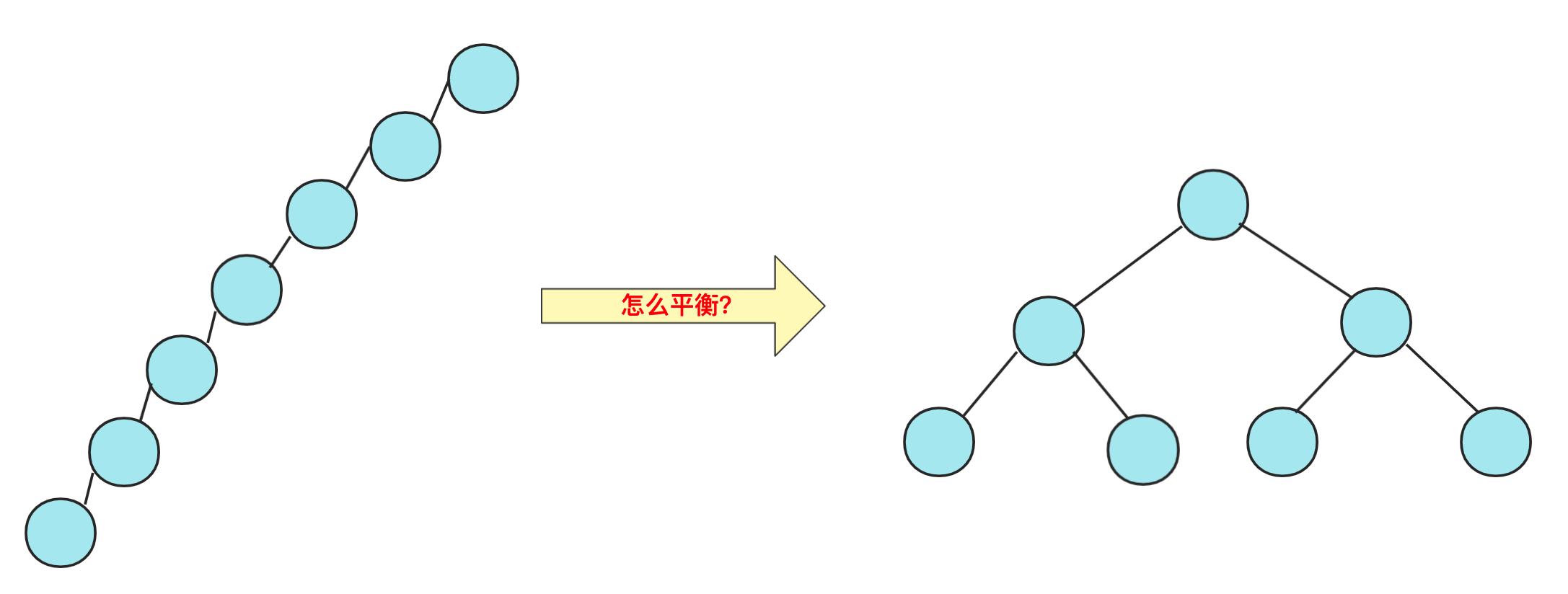
对于树这种数据结构,我们通常将其分为二叉树和多叉树两大类。在二叉树中,我们熟知的包括二叉搜索树、二叉平衡树、伸展树、红黑树等。多叉树中,经典的例子有B树和字典树。
二叉搜索树具有这样的特点:每个节点都有左孩子和右孩子,且左侧节点值小于父节点值,右侧节点值大于父节点值。这样的特性就使得二叉搜索树在数值查找方面有一些价值,比较好的查找情况时间复杂度是O(logn)。
然而,二叉搜索树存在一个明显的问题:当插入节点的顺序过于有序时,很容易导致树形成斜树或深度较高的情况,使得查找效率趋近于线性O(n)。
为了解决这一问题,人们希望二叉树能够保持插入节点时的有序性,即小的节点在左侧,大的节点在右侧,但又避免出现斜树那么离谱的情况。这就引出了对平衡性的需求,即希望树的结构能够在插入操作后自动保持平衡,以提高整体的查找效率。这需求推动了平衡二叉树的概念,它们通过一系列规则和旋转操作来确保树的平衡性,从而兼顾了有序性和高效查找的要求。
这不,平衡二叉搜索(AVL)树就是这么干的,AVL树在插入的时候每次都会旋转自平衡,让整个树一直处于平衡状态,让整个树的查询更加稳定(logN)。我们首先来看一下什么是ALV树:
- AVL树是带有平衡条件的二叉搜索树,左右子树的高度差(平衡因子)不大于1,并且它的每个子树也都是平衡二叉树。
对于平衡二叉树节点的最小个数求法,类似求斐波那契:
节点个数=F(h)=F(h−1)+F(h−2)+1
F(0)=0
F(1)=2
其中,F(h) 表示高度为 h 的平衡二叉树的最小节点个数,F(h−1) 表示高度为 h-1 的平衡二叉树的最小节点个数,F(h−2) 表示高度为 h-2 的平衡二叉树的最小节点个数。
基本上,这个公式是一个斐波那契数列的变种,通过递归关系计算出高度为 h 的最小节点个数。
一个更直观的解释是:对于一棵平衡二叉树,每个节点都有左右两个子节点,因此高度为 h 的树至少包含高度为 h-1 和 h-2 的两个子树,再加上根节点,所以节点个数可以表示为左右子树节点个数之和再加1。
难点:AVL是一颗二叉排序树,用什么样的规则或者规律让它能够在复杂度不太高的情况下实现动态平衡呢?
如果从简单情况模型看,其实四种不平衡情况很简单,分别是RR,LL,RL,LR四种不平衡情况。
然后将其平衡的结果也很容易(不考虑其附带节点只看结果),将中间大小数值移动最上方,其他相对位置不变即可:
当然,这个仅仅是针对三个节点情况太过于理想化了,很多时候树的结构比较复杂有较多子节点和父节点,我们需要针对整个流程梳理一下如何保持一个二叉平衡树。
首先,刚开始树是平衡的。
前面的若干次操作,都是平衡的,然后可能因为某一次操作突然使得这个AVL树不满足(每个节点),然后我们就要详细思考一下这次操作需要怎么搞。
插入可以采用一个递归的方式(如果不采用递归可能会借助一个新的父节点去实现),然后在递归向下的时候,我们正常的插入节点。
被插入的那个节点,因为没有儿子节点,所以肯定是满足平衡条件的,然后后面就进入递归回去的过程,回去的过程中,需要对每个节点更新深度,并且判断当前节点是否平衡,如果不平衡,需要将节点平衡了然后继续,至于细节,下面详细介绍。
针对四种不平衡的情况,这里对每种情况进行详细的讲解。
到达递归oldroot时候发现不平衡了(左右子孩子都是平衡的),这里的RR指的是节点模型的样子,其含义是需要左单旋转(记忆时候需要注意一下RR不是右旋转)!
出现这种情况的原因是节点的右侧的右侧较深这时候不平衡节点需要左旋,再细看过程。
我们分析一下这种情况:可能新插入节点在newroot右侧,然后newroot也满足平衡,左右的深度分别为H和H+1。
但是此时oldroot左侧依然是H,但是右侧已经变成H+2,显然不满足但是差距又不大(刚开始出现不平衡的情况说不定微调就可以)。
这里也是一棵二叉排序树哦,根节点数值大小顺序为:
红H < oldroot < 绿H < newroot < 蓝色H+1
所以调整平衡这里面newroot作为根做合理,然后比它小的都要放到左侧,刚好oldroot作为左儿子那么它的右侧空出来,这个绿H刚好满足在它右侧,这样调整就满足左单旋转了。在执行完毕只有oldroot和newroot的高度发生了变化,其他节点高度未发生变化。
其更详细流程为:
而右旋和左旋相反,但是思路相同,根据上述进行替换即可!
这个RL你可能有点懵圈,为啥RR叫左旋,LL叫右旋,这个RL怎么就叫先右后左旋转了?
别急别急,这个之所以先右后左,是因为具体需要中间节点右旋一次,然后上面节点左旋一次才能平衡,具体可以下面慢慢看。
首先产生这种不平衡的条件原因是:
仅有当前ROOT不平衡,且是ROOT.right.left这个节点深了一些(这个节点可能有个节点深一点或者两个节点都深一点),例如下面三种情况:
但其实并不影响,还是因为R.L这个节点深了一些。平衡方式的其实可以窥见:root和橙色H高度H+1,R和绿色H高度为H+1,这两个节点分别放在R.L左右,然后接上R.L本身的两个孩子,这样刚好平衡且满足条件。
该怎么做呢?
两次上浮,之前左旋右旋一次操作可以上浮平衡一位,这次先对R进行右旋操作,R.L上浮到ROOT右侧,此时右侧变深了满足RR左单旋转情况,对root开始左旋,就完成操作实现平衡。
思路(个人方法)2:直接分析
根据初始和结果的状态,然后分析各个节点变化顺序=,手动操作这些节点即可。其实不管你怎么操作,只要能满足最后结构一致就行啦!
首先根据ROOT,R,R.L三个节点变化,R.L肯定要在最顶层,左右分别指向ROOT和R,那么这其中R.left,ROOT.right发生变化(原来分别是R.L和R)暂时为空。而刚好根据左右大小关系可以补上R.L原来的孩子节点A,B。
这个情况和RL情况相似,采取相同操作即可。
根据上述RL修改即可
首先对于节点多个height属性。用于计算高度(平衡因子)
public class AVLTree {
class TreeNode {
int value;
int height; // 节点的高度,用于平衡因子计算
TreeNode left;
TreeNode right;
public TreeNode(int value) {
this.value = value;
this.height = 1; // 初始高度为1
this.left = null;
this.right = null;
}
}
private TreeNode root;
// 获取节点的高度
private int height(TreeNode node) {
return (node != null) ? node.height : 0;
}
// 计算平衡因子
private int getBalanceFactor(TreeNode node) {
return (node != null) ? height(node.left) - height(node.right) : 0;
}
// 更新节点的高度
private void updateHeight(TreeNode node) {
if (node != null) {
node.height = 1 + Math.max(height(node.left), height(node.right));
}
}
// 右旋转操作 返回操作完的新节点
private TreeNode rightRotate(TreeNode oldRoot) {
TreeNode newRoot = oldRoot.left;
TreeNode temp = newRoot.right;
// 执行旋转
newRoot.right = oldRoot;
oldRoot.left = temp;
// 更新节点高度 其他节点的高度并没有更新
updateHeight(oldRoot);
updateHeight(newRoot);
// 返回新的根节点
return newRoot;
}
// 左旋转操作 返回操作完的新节点
private TreeNode leftRotate(TreeNode oldRoot) {
TreeNode newRoot = oldRoot.right;
TreeNode temp = newRoot.left;
// 执行旋转
newRoot.left = oldRoot;
oldRoot.right = temp;
// 更新节点高度 先更新低层的
updateHeight(oldRoot);
updateHeight(newRoot);
// 返回新的根节点
return newRoot;
}
// 插入节点
public void insert(int value) {
root = insert(root, value);
}
// 辅助方法:插入节点(递归)
private TreeNode insert(TreeNode node, int value) {
// 执行标准BST插入
if (node == null) {
return new TreeNode(value);
}
if (value < node.value) {
node.left = insert(node.left, value);
} else if (value > node.value) {
node.right = insert(node.right, value);
} else {
// 重复值不允许插入(可以根据实际需求进行调整)
return node;
}
// 更新节点的高度
updateHeight(node);
// 获取平衡因子
int balance = getBalanceFactor(node);
// 进行平衡操作
// 左子树比右子树高,需要右旋转
if (balance > 1 && value < node.left.value) {
return rightRotate(node);
}
// 右子树比左子树高,需要左旋转
if (balance < -1 && value > node.right.value) {
return leftRotate(node);
}
// 左右不平衡,先左旋后右旋
if (balance > 1 && value > node.left.value) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// 右左不平衡,先右旋后左旋
if (balance < -1 && value < node.right.value) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 中序遍历(用于验证树的平衡性)
public void inOrderTraversal(TreeNode node) {
if (node != null) {
inOrderTraversal(node.left);
System.out.print(node.value + " ");
inOrderTraversal(node.right);
}
}
public static void main(String[] args) {
AVLTree avlTree = new AVLTree();
// 插入一些节点
avlTree.insert(10);
avlTree.insert(20);
avlTree.insert(30);
avlTree.insert(40);
avlTree.insert(50);
avlTree.insert(25);
// 中序遍历输出,验证平衡性
avlTree.inOrderTraversal(avlTree.root);
}
}AVL的理解需要时间,当然笔者的AVL自己写的可能有些疏漏,如果有问题还请各位一起探讨!
当然,除了插入,AVL还有删除等其他操作,(原理相似。删除后平衡)有兴趣可以一起研究。