@TOC
微信公众号:
bigsai数据结构与算法专栏
在排序中,我们可能大部分更熟悉冒泡排序、快排之类。对归并排序可能比较陌生。然而事实上归并排序也是一种稳定的排序,时间复杂度为O(nlogn).
归并排序是基于分治进行归并的,有二路归并和多路归并.我们这里只讲二路归并并且日常用的基本是二路归并。并且归并排序的实现方式有递归形式和非递归形式。要注意其中的区分(思想上没有大的区别,只是划分上会有区分后面会对比)。
并且归并排序很重要的一个应用是求序列中的逆序数个数。当然逆序数也可以用树状数组完成,这里就不介绍了。
归并和快排都是基于分治算法的。分治算法其实应用挺多的,很多分治会用到递归,也有很多递归实现的算法是分治,但事实上分治和递归是两把事。分治就是分而治之。因为面对排序,如果不采用合理策略。每多一个数就会对整个整体带来巨大的影响。而分治就是将整个问题可以分解成相似的子问题。子问题的解决要远远高效于整个问题的解决,并且子问题的合并并不占用太大资源。
至于归并的思想是这样的:
- 第一次:整串先进行划分成1个一个单独,第一次是一一(
12 34 56---)归并成若干对,分成若干2个区间.归并完(xx xx xx xx----)这样局部有序的序列。 - 第二次就是两两归并成若干四个(
1234 5678 ----)每个小局部是有序的。 - 就这样一直到最后这个串串只剩一个,然而这个耗费的总次数logn。每次操作的时间复杂的又是
O(n)。所以总共的时间复杂度为O(nlogn).
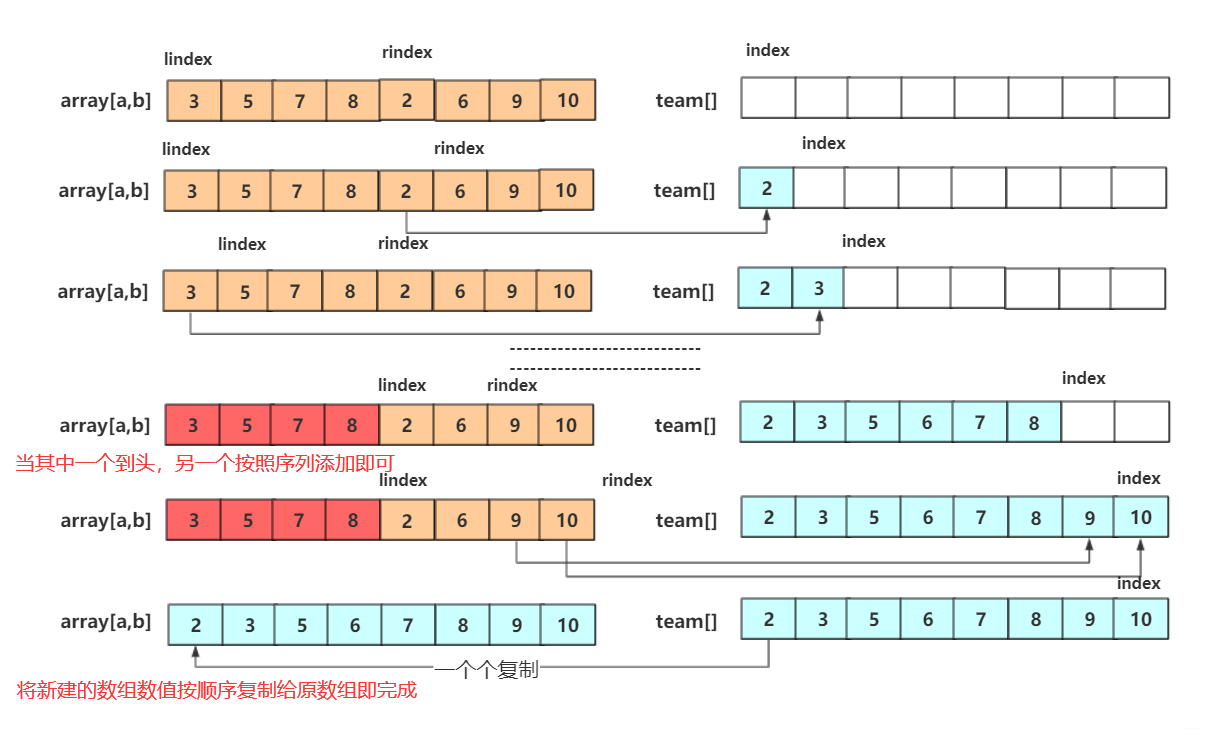
对于分治过程你可能了解了,但是这个两两merge的过程其实是很重要的。首先我们直到的两个序列都是有序的。其实思想也很简单,假设两个串串为 3 5 7 8和2 6 9 10进行归并操作。我们需要借助一个额外的数组team[8]将两个串串有序存进去就行。而流程是这样的:
非递归的归并
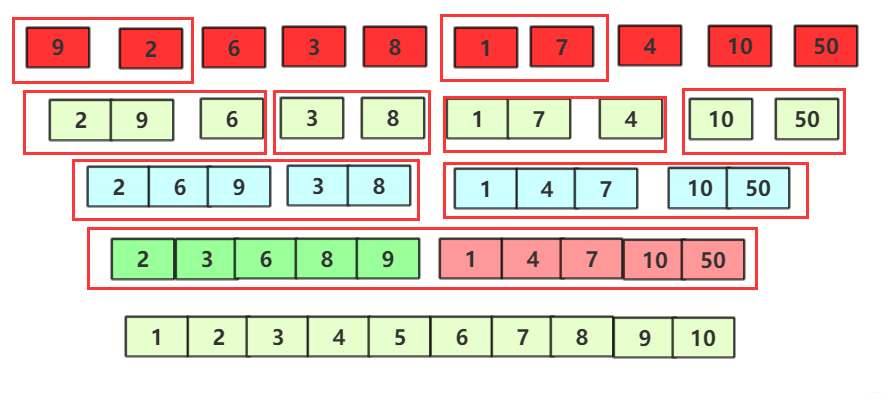
正常归并的代码实现都是借助递归的。但是也有不借助递归的。大部分课本或者考试如果让你列归并的序列,那么默认就是非递归的,比如一个序列9,2,6,3,8,1,7,4,10,5序列的划分也是这样的。
第一次结束: {2,9}{3,6}{1,8}{4,7}{5,10}
第二次结束:{2,3,6,9}{1,4,7,8}{5,10}
第三次结束:{1,2,3,4,6,7,8,9}{5,10}
第四次结束:{1,2,3,4,5,6,7,8,9,10}递归的归并
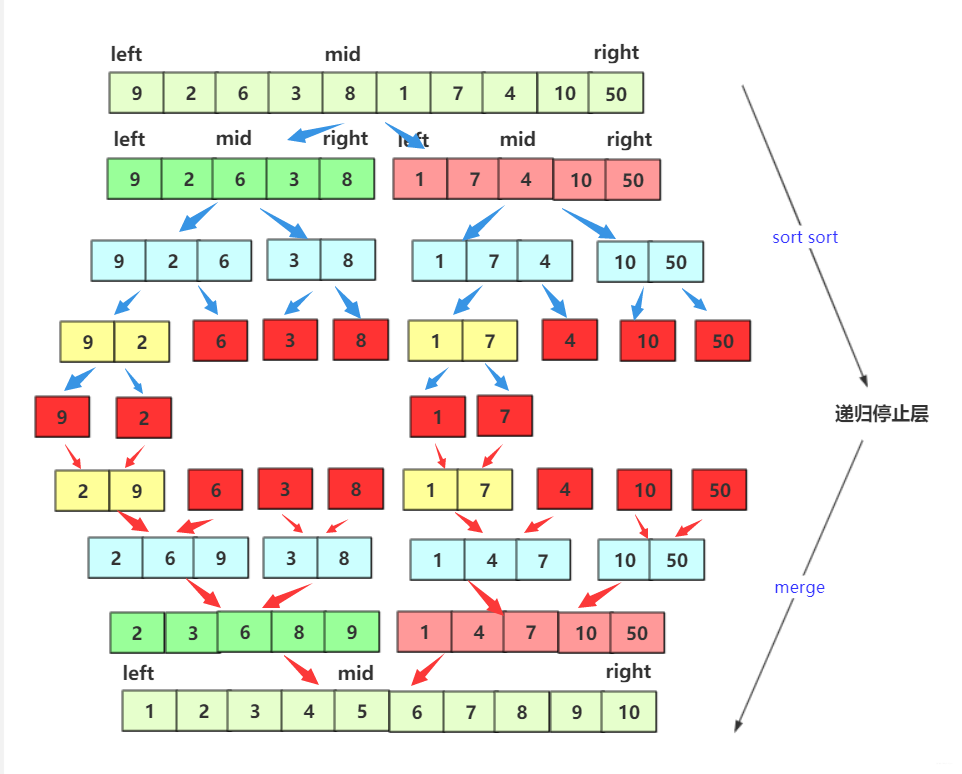
在代码实现上的归并可能大部分都是递归的归并。并且递归和分治整在一起真的是很容易理解。递归可以将问题分解成子问题,而这恰恰是分治所需要的手段。而递归的一来一回过程的来(分治)回(归并),一切都刚刚好。
而递归的思想和上面非递归肯定不同的,你可以想想非递归:我要考虑当前几个进行归并,每个开始的头坐标该怎么表示,还要考虑是否越界等等问题哈,写起来略麻烦。
而非递归它的过程就是局部—>整体的过程,而递归是整体—>局部—>整体的过程。
而递归实现的归并的思想:
void mergesort(int[] array, int left, int right) {
int mid=(left+right)/2;//找到中间节点
if(left<right)//如果不是一个节点就往下递归分治
{
mergesort(array, left, mid);//左区间(包过mid)进行归并排序
mergesort(array, mid+1, right);//右区间进行归并排序
merge(array, left,mid, right);//左右已经有序了,进行合并
}
}同样是9,2,6,3,8,1,7,4,10,5这么一串序列,它的递归实现的顺序是这样的(可能部分有点问题,但是还是有助于理解的):
所以实现一个归并排序的代码为:
private static void mergesort(int[] array, int left, int right) {
int mid=(left+right)/2;
if(left<right)
{
mergesort(array, left, mid);
mergesort(array, mid+1, right);
merge(array, left,mid, right);
}
}
private static void merge(int[] array, int l, int mid, int r) {
int lindex=l;int rindex=mid+1;
int team[]=new int[r-l+1];
int teamindex=0;
while (lindex<=mid&&rindex<=r) {//先左右比较合并
if(array[lindex]<=array[rindex])
{
team[teamindex++]=array[lindex++];
}
else {
team[teamindex++]=array[rindex++];
}
}
while(lindex<=mid)//当一个越界后剩余按序列添加即可
{
team[teamindex++]=array[lindex++];
}
while(rindex<=r)
{
team[teamindex++]=array[rindex++];
}
for(int i=0;i<teamindex;i++)
{
array[l+i]=team[i];
}
}首先得了解什么是逆序数:
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对
也就是比如3 2 1.看3 ,有2 1在后面,看2 有1在后面有3个逆序数。
而比如1 2 3的逆序数为0.
在数组中,暴力确实可以求出逆序数,但是暴力之法太复杂,不可取!而有什么好的方法能解决这个问题呢? 当前序列我可能不知道有多少序列。但是我们直到如果这个序列如果有序那么逆序数就为0.
在看个序列 abcd 3 2 1 efg编程abcd 1 2 3 efg整个序列逆序数减少3个。因为如果不管abcd还是efg和123三个数相对位置没有变。所以我们是可以通过某种方法确定逆序数对的。
我们就希望能不能有个过程,动态改变如果逆序数发生变化能够记录下来?!比如动那么一下能够知道有没有改变的。并且这个动不能瞎动,最好是局部的,有序的动。归并排序就是很适合的一个结构。因为肯定要选个小于O(n^2^)的复杂度算法,而归并排序满足,并且每次只和邻居进行归并,归并后该部分有序。
纵观归并的每个单过程例如两个有序序列:假设序列2 3 6 8 9和序列1 4 7 10 50这个相邻区域进行归并。
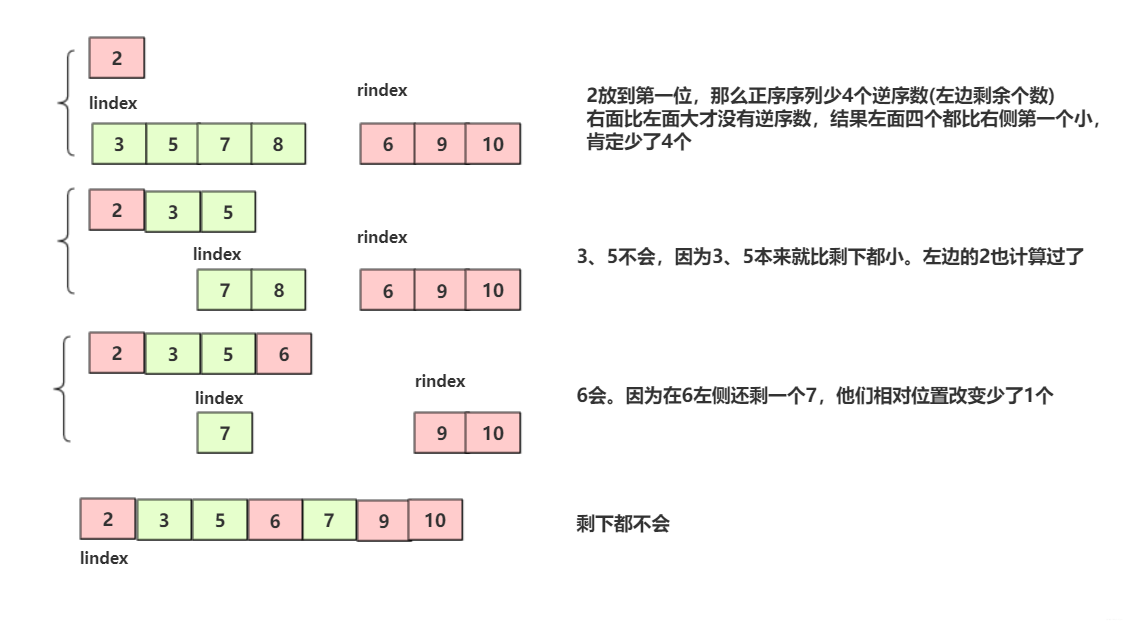
至于规律,你可以发现每次归并过程中,当且仅当右侧的数提前放到左侧,而左侧还未放置的个数就是该元素减少的逆序个数! 这个需要消化一下,而在代码实现中,需要这样进行即可!
int value;
------
-----
------
private static void merge(int[] array, int l, int mid, int r) {
int lindex=l;int rindex=mid+1;
int team[]=new int[r-l+1];
int teamindex=0;
while (lindex<=mid&&rindex<=r) {
if(array[lindex]<=array[rindex])
{
team[teamindex++]=array[lindex++];
}
else {
team[teamindex++]=array[rindex++];
value+=mid-lindex+1;//加上左侧还剩余的
}
}
while(lindex<=mid)
{
team[teamindex++]=array[lindex++];
}
while(rindex<=r)
{
team[teamindex++]=array[rindex++];
}
for(int i=0;i<teamindex;i++)
{
array[l+i]=team[i];
}
}原创不易,最后我请你帮两件事帮忙一下:
-
star支持一下, 您的肯定是我在平台创作的源源动力。
-
微信搜索「bigsai」,关注我的公众号,不仅免费送你电子书,我还会第一时间在公众号分享知识技术。加我还可拉你进力扣打卡群一起打卡LeetCode。
记得关注、咱们下次再见!