s0101_symmetric_tree

101. Symmetric Tree

Easy

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

Example 1:

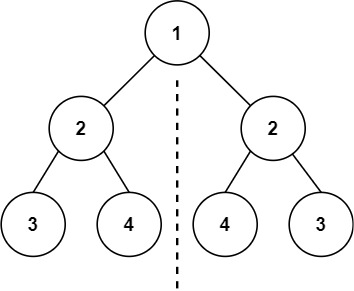
Input: root = [1,2,2,3,4,4,3]

Output: true

Example 2:

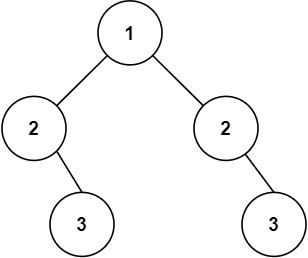
Input: root = [1,2,2,null,3,null,3]

Output: false

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• -100 <= Node.val <= 100

Follow up: Could you solve it both recursively and iteratively?

To solve the "Symmetric Tree" problem in Java with the Solution class, follow these steps:

1. Define a method isSymmetric in the Solution class that takes the root of a binary tree as input and returns true if the tree is symmetric, and false otherwise.
2. Implement a recursive approach to check if the given binary tree is symmetric:
   • Define a helper method isMirror that takes two tree nodes as input parameters.
   • In the isMirror method, recursively compare the left and right subtrees of the given nodes.
   • At each step, check if the values of the corresponding nodes are equal and if the left subtree of one node is a mirror image of the right subtree of the other node.
   • If both conditions are satisfied for all corresponding nodes, return true; otherwise, return false.
3. Call the isMirror method with the root's left and right children to check if the entire tree is symmetric.

Here's the implementation of the isSymmetric method in Java:

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        return isMirror(root.left, root.right);
    }
    
    private boolean isMirror(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true;
        }
        if (left == null || right == null) {
            return false;
        }
        return (left.val == right.val) && isMirror(left.left, right.right) && isMirror(left.right, right.left);
    }
}

This implementation recursively checks whether the given binary tree is symmetric around its center in O(n) time complexity, where n is the number of nodes in the tree.