Constrained iterations, and Datalog-like recursion

[julianhyde]

Morel has successfully integrated many aspects of relational languages into a functional programming language but a good syntax for recursively defined relations has been elusive. This is all the more surprising given that recursive relations are so easily defined in Datalog, a simpler language based on the deductive paradigm.

We propose a new Morel language concept, named 'constrained iteration' and introduced by a new suchThat keyword, that allows relations (including recursive relations) to be defined in a similar way to Datalog. This concept fits elegantly with the rest of Morel, gives Morel the same power as Datalog, and gives the Morel program authors more flexibility in how they structure their programs without sacrificing any power or efficiency.

To solve the mystery of why Datalog is different, we journey through set theory, how mathematics and computer science define functions, and the relationship between fixed-points and recursively-defined functions.

Two families of data languages

Deductive data languages (such as Datalog) and data languages based on relational algebra (such as SQL, Morel, Datafun) do much the same thing, but go about it in different ways.

Even though their paradigms are different, for many operations, such as joining and filtering, the code in the deductive language (Datalog) will tend have a similar size and structure to the code in the language based on relational algebra (Morel).

When recursion is involved, the languages part ways - Datalog generally seems to be more concise - but first of all, let's explore why programs in the two languages tend to look so similar, most of the time. It goes back to set theory.

In set theory, there are two ways of defining a set: intensional and extensional. Wikipedia gives the following definitions:

• An intensional definition gives meaning to a term by specifying necessary and sufficient conditions for when the term should be used.
• An extensional definition gives meaning to a term by specifying its extension, that is, every object that falls under the definition of the term in question.

Let's suppose you want to make the set of red bicycles, RB.

Type	Definition
Intensional definition	An object is in RB if it is a bicycle and it is red. Furthermore, it is a bicycle if it is a vehicle and has two wheels.
Extensional definition	RB is the intersection of R, the set of red objects, and B, the set of bicycles. B is the intersection of V, the set of vehicles, and W2, the set of objects with two wheels.

These expressions map to programs in Datalog and Morel:

Datalog (intensional)	red_bicycle(x) :- bicycle(x), red(x). bicycle(x) :- vehicle(x), x.wheel_count = 2.
Morel (extensional)	val bicycles = from v in vehicles where v.wheelCount = 2 val redObjects = from o in allObjects where o.color = 'red' val redBicycles = bicycles intersect redObjects

The programs have similar structure, because each operation on an extensional set has a corresponding operator on an intensional set. For example, where Datalog uses "," (boolean AND), Morel uses "intersect".

The duality is very clear when we draw the sets in a Venn diagram:

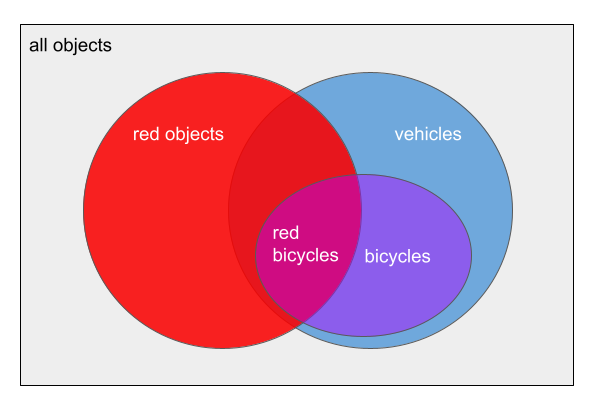
Venn diagrams are powerful visualizations because, where the dualism is concerned, they don't pick sides. You can interpret the red area intensionally (objects whose color property has the value 'red') and extensionally (the set of all red objects). The duality isn't created by Venn diagrams, or languages such as Datalog or Morel; it has been in set theory from the start.

The relational data model, based on set theory, recognized the duality from the start: Codd's theorem proved that domain-independent relational calculus is equivalent to relational algebra. Datalog is a descendant of relational calculus, and has an elegant means to recursively define relations; the descendants of relational algebra have better handling of multisets, aggregation, and nested relations, but their handling of recursive relations is clunky.

Extents

Observe that the Morel program uses an allObjects collection that has no analog in the Datalog program. An extensional language such as Morel needs to start with an extent - the set of all objects of a particular type, such as the set of all red objects or the set of all vehicles - whereas an intensional language just needs to define a predicate, saying, in effect, 'hand me an object and I'll tell you whether it is red'.

In practice, extensional programs limit themselves to a finite extent ("the set of vehicles that I own") and mix in some intensional logic ("I know we're working with vehicles here, so give me the set of vehicles and I'll give you back the ones that are red"). But I claim that, by forcing a programmer to choose between intensional or extensional thinking, the language is doing no one any favors. The programmer may have to rewrite code if it turns out that the extent they need is no longer available. And the runtime is forced to execute the program the way the programmer wrote it, even though the other way might be more efficient.

If we could remove the need for this forced switching, would we make it easier to write programs? Let's come back to that question after we look at the one area where deductive and relational languages are significantly different: recursion.

Recursion

A simple example (based on the Datafun: a functional Datalog paper) illustrates recursion. The Morel variable parents is a relation that contains parent-child relationships:

- val parents =
    [("earendil", "elrond"), ("elrond", "elladan"),
      ("elrond", "elrohir"), ("elrond", "arwen")];
val parents : string * string list

How can we write a Morel function that returns the set of (x, y) pairs such that x is an ancestor of y? Our first attempt, inspired by SQL's WITH RECURSIVE construct, is to write a recursive function that uses union:

- fun ancestors () =
    (from (x, y) in parents yield (x, x))
    union
    (from (x, y) in parents,
        (y2, z) in ancestors ()
      where y = y2
      yield (x, z));
val ancestors = fn : unit -> (string * string) list

But when we run it we get a stack overflow! It's not surprising when you notice that ancestors calls itself recursively with the same arguments that it was invoked with. While it's valid in mathematics to define a function in terms of itself, this is no way to write a function in a programming language.

Our next thought was to teach Morel that the union is somehow special, add some notion of monotonicity to the type system, and allow the language to deduce when recursive functions involving union proceed towards a fixed point. This seems rather complicated. (How much effort would be required by the user to specify monotonicity? Are there other functions besides union that have monotonic behavior? Would we allow users to define their own monotonic functions and types?)

How does Datalog solve the problem? The following program defines an is_parent base relation, and a recursively derived is_ancestor relation.

is_parent(earendil, elrond).
is_parent(elrond, arwen).
is_parent(elrond, elladan).
is_parent(elrond, elrohir).
is_ancestor(X, Y) :- is_parent(X, Y).
is_ancestor(X, Y) :- is_parent(X, Z), is_ancestor(Z, Y).

Why is Datalog more concise? Datalog is operating on boolean values (predicates) rather than sets. Whereas the Morel function was invoked with a unit argument and returned a set, Datalog functions were invoked with specific arguments (and invoked many times, once for each value in a set) and returned a boolean.

In mathematics, a relation is a set of n-tuples. A Datalog rule tests membership of a relation. For example, when we invoke is_ancestor(earendil, arwen) we are asking whether (earendil, arwen) belongs to the relation.

A mathematical function is a special kind of relation - it is a binary relation whose pairs' left elements are unique - and it is well known that in lambda calculus we can define recursive functions using a fixed-point combinator. It is less often remembered that the 'fixed point' being computed is not the result of a particular call to the function, but the function itself, namely the set of (argument, result) pairs.

If we are going to recursively define relations, then it makes sense to use the same approach. And in fact Datalog does just that. It deduces the contents of a relation by starting with a set of base facts, then applies all possible rules to deduce new facts until it cannot deduce any more. The process converges in a straightforward way because the boolean value - the proof that a tuple is in the relation - is monotonic.

We had trouble making the ancestors Morel function recursive because it was trying to work on sets (where monotonicity is not trivial as it is for bool) and because each iteration was not just deducing a result for an argument value for which the function was previously undefined.

So, let's abandon that approach. Let's make it possible in Morel to define sets based on a predicate.

Constrained iteration

We propose a new operator suchThat, to make a new clause in the from expression. This clause performs what we call 'constrained iteration' (iteration of variables over the values for which a predicate is true), as opposed to the usual iteration over the values of a list- or set-valued expression.

Syntax is as follows:

exp →           (* other expressions *)
  | from [ scan1  , ... , scans ] step*
                              relational expression (s ≥ 0)
scan → pat [ in | = ] exp
  | id1 , ... , idi suchThat exp
                              constrained iteration (i ≥ 1)
step → where exp                filter clause
  | join scan [ on exp ]      join clause
  | group groupKey1 , ... , groupKeyg
    [ compute agg1 , ... , agga ]
                              group clause (g ≥ 0, a ≥ 1)
  | compute agg1 , ... , agga
                              compute clause (a > 1)
  | order orderItem1 , ... , orderItemo
                              order clause (o ≥ 1)
  | yield exp

The following query computes the set of job titles that are managed by employees in department 20:

- fun isManagerOf (e, job) =
    exists (from e2 in emps
      where e2.mgrno = e.empno
      andalso e2.job = job);
val isManagerOf = fn : Emp * string -> bool
- from e in emps,
      job suchThat isManagerOf (e, job)
    where d.deptno = 20
    yield job;
val it : string list

The function isManagerOf returns whether employee e manages someone with job title job.

The clause job suchThat isManagerOf (e, job) does something strange. It apparently iterates over all possible jobs, and then checks whether the current employee e manages someone with that job.

The set of all possible jobs is infinite, the implementation does not literally iterate over all possible jobs. It drives in the other direction, starting with the set of jobs that actually exist, and constraining e to be the manager of people with those jobs. If there is no source of values, there is nothing to drive from, and Morel
rejects the query as unimplementable. For example:

- from (e, job) suchThat isManagerOf (e, job)
    yield job;
Error: Argument to suchThat is insufficiently constrained

It is OK to define a function that is insufficiently constrained, but you can only call that function from a top-level query if there are sufficient constraints.

When sufficiently constrained, by passing in a value of e that is iterating over a finite extent, isManagerOf is in effect just defining a 'managerJobs' relation, but is doing it in the 'backwards' Datalog manner of writing a bool function.

When defining a relation, there is no preferred direction: sometimes the most natural formulation uses a set-valued expression, in which case you would use forward clause (with in or =); sometimes it is a boolean-valued expression, in which case you would use a backwards clause (suchThat). Morel's optimizer is equally happy with either, and can take a query with a mixture of forwards and backwards clauses and find an efficient plan.

Recursively defined relations

When defining recursive queries, backwards is the preferred direction. Let's return to the problem of recursively defining the ancestors relation. The definition is much more concise using a 'backwards' function isAncestor:

- fun isParent (x, y) =
    (x, y) elem parents;
val isParent = fn : string * string -> bool
- fun isAncestor (x, y) =
    isParent (x, y)
    orelse exists (
      from z suchThat isParent (x, z) andalso isAncestor (z, y));
val isAncestor = fn : string * string -> bool

Note how the z suchThat clause in the isAncestor function introduces a variable z and iterates over all possible values of z where the boolean expression isParent (x, z) andalso isAncestor (z, y) is true. We call this 'constrained iteration'.

Constrained iteration is only allowed if Morel can deduce a finite extent for the variable. In this case, the iteration is safe. By looking inside the definition of the isParent function, Morel's compiler can deduce that z only takes the the values that occur in on the right-hand side of the parent relation, namely "elrond", "arwen", "elladan", "elrohir".

One the isAncestor function is defined, we can use it in several ways:

- isAncestor ("earendil", "arwen");
val it = true : bool
- isAncestor ("arwen", "elladan");
val it = false : bool
- from x suchThat isAncestor (x, "arwen");
val it = ["earendil", "elrond", "arwen"] : string list
- from y suchThat isAncestor ("elrond", y);
val it = ["elrond", "arwen", "elladan", "elrohir"] : string list
- from (x, y) suchThat  isAncestor (x, y);
val it =
  [("earendil", "earendil"), ("earendil", "elrond"), ("earendil", "arwen"),
   ("earendil", "elladan"), ("earendil", "elrohir"), ("elrond", "elrond"),
   ("elrond", "arwen"), ("elrond", "elladan"), ("elrond", "elrohir"),
   ("arwen", "arwen"), ("elladan", "elladan"), ("elrohir", "elrohir")]
 : (string * string) list

The last of these is the most interesting. By generating both arguments to isAncestor in a suchThat clause, we have told Morel to generate the entire ancestors relation.

Related work

Flix is another functional language that incorporates Datalog. Datalog-style constraints are first-class values, but they are defined in a sub-language and therefore interoperation with other language features is somewhat limited.

Datafun is a functional language with relational extensions. It added recursion by making monotonicity a first-class property of every type, and can thereby prove that recursive computations on sets are guaranteed to terminate. Recursive computations are implemented efficiently by rewriting them to use seminaïve evaluation, the same mechanism used by most Datalog implementations.

Conclusion

Constrained iteration brings Datalog-like expressive power to Morel, and provides a natural and concise way to recursively define relations. The feature can be freely mixed with other language features such as function declarations, patterns and polymorphic types, and gives Morel's compiler/optimizer freedom to find the most efficient implementation of a data-parallel program.

Note that constrained iteration and the suchThat keyword are proposed language features and are not implemented. Some of the examples require either annotation or inference of record-valued argument types, which is also not implemented.

[julianhyde]

I discuss this topic in my talk Is there a perfect data-parallel programming language?. See section 5, 'Functional + Deductive'.