diff --git a/biocintro_5x/bioc1_liftOver.Rmd b/biocintro_5x/bioc1_liftOver.Rmd
index 8f12ed4a..4ebc7833 100644
--- a/biocintro_5x/bioc1_liftOver.Rmd
+++ b/biocintro_5x/bioc1_liftOver.Rmd
@@ -68,7 +68,7 @@ ah = AnnotationHub()
q1 = query(ah, c("chain")) # list all resources with 'chain' in metadata
q1
q2 = query(ah, c("chain", "hg38ToHg19")) # the one we want
-ch = ah[[names(q2)]]
+ch = ah[[names(q2)[1]]]
```
```{r domyimport}
diff --git a/biocintro_5x/bioc1_roast.Rmd b/biocintro_5x/bioc1_roast.Rmd
index 82bd690e..b32897c2 100644
--- a/biocintro_5x/bioc1_roast.Rmd
+++ b/biocintro_5x/bioc1_roast.Rmd
@@ -31,7 +31,7 @@ Briefly, the investigators applied a glucocorticoid hormone to cultured human ai
The groups are defined in the `characteristics_ch1.2` variable:
```{r}
-e$condition <- e$characteristics_ch1.2
+e$condition <- as.factor(e$characteristics_ch1.2)
levels(e$condition) <- c("dex24","dex4","control")
table(e$condition)
```
@@ -128,7 +128,7 @@ columns(GO.db)
keytypes(GO.db)
GOTERM[[rownames(r2)[1]]]
r2tab <- select(GO.db, keys=rownames(r2)[1:10],
- columns=c("GOID","TERM","DEFINITION"),
+ columns=c("GOID","TERM","DEFINITION"),
keytype="GOID")
r2tab[,1:2]
```
@@ -138,7 +138,7 @@ We can also look for the top results using the standard p-value and in the *up*
```{r}
r2 <- r2[order(r2$PValue),]
r2tab <- select(GO.db, keys=rownames(r2)[r2$Direction == "Up"][1:10],
- columns=c("GOID","TERM","DEFINITION"),
+ columns=c("GOID","TERM","DEFINITION"),
keytype="GOID")
r2tab[,1:2]
```
@@ -147,7 +147,7 @@ Again but for the *down* direction.
```{r}
r2tab <- select(GO.db, keys=rownames(r2)[r2$Direction == "Down"][1:5],
- columns=c("GOID","TERM","DEFINITION"),
+ columns=c("GOID","TERM","DEFINITION"),
keytype="GOID")
r2tab[,1:2]
```
diff --git a/biocintro_5x/bioc1_t_mult.Rmd b/biocintro_5x/bioc1_t_mult.Rmd
index 4b692ee7..31a0d750 100644
--- a/biocintro_5x/bioc1_t_mult.Rmd
+++ b/biocintro_5x/bioc1_t_mult.Rmd
@@ -32,11 +32,11 @@ In this section we will cover inference in the context of genome-scale experimen
- there may be unmeasured or unreported sources of biological variation (such as time of day)
- many features are inherently interrelated, so the tests are not independent
-We will apply some of the concepts we have covered in previous
+We will apply some of the concepts we have covered in previous
sections including t-tests and multiple comparisons; later we will
-compute standard deviation estimates from hierarchical models.
+compute standard deviation estimates from hierarchical models.
-We start by loading the pooling experiment data
+We start by loading the pooling experiment data
```{r,message=FALSE}
@@ -68,7 +68,7 @@ tt=rowttests(y,g)
```
-Now which genes do we report as statistically significant? For somewhat arbitrary reasons, in science p-values of 0.01 and 0.05 are used as cutoff. In this particular example we get
+Now which genes do we report as statistically significant? For somewhat arbitrary reasons, in science p-values of 0.01 and 0.05 are used as cutoff. In this particular example we get
```{r}
NsigAt01 = sum(tt$p.value<0.01)
@@ -90,17 +90,18 @@ set.seed(0)
shuffledIndex <- factor(sample(c(0,1),sum(g==0),replace=TRUE ))
nulltt <- rowttests(y[,g==0],shuffledIndex)
NfalselySigAt01 = sum(nulltt$p.value<0.01)
-NfalselySigAt01
+NfalselySigAt01
NfalselySigAt05 = sum(nulltt$p.value<0.05)
NfalselySigAt05
```
-If we use the 0.05 cutoff we will be reporting `r NfalselySigAt05` false positives. We have described several ways to adjust for this including the `qvalue` method available in the `r Biocpkg("qvalue")` package. After this adjustment we acquire
+If we use the 0.05 cutoff we will be reporting `r NfalselySigAt05` false positives. We have described several ways to adjust for this including the `qvalue` method available in the `r Biocpkg("qvalue")` package. After this adjustment we acquire
a smaller list of genes.
```{r}
+library(BiocStyle)
library(qvalue)
qvals = qvalue(tt$p.value)$qvalue
sum(qvals<0.05)
diff --git a/highdim/distance.Rmd b/highdim/distance.Rmd
index 8bd6594f..74d42f25 100644
--- a/highdim/distance.Rmd
+++ b/highdim/distance.Rmd
@@ -14,11 +14,11 @@ opts_chunk$set(fig.path=paste0("figure/", sub("(.*).Rmd","\\1",basename(knitr:::
The concept of distance is quite intuitive. For example, when we cluster animals into subgroups, we are implicitly defining a distance that permits us to say what animals are "close" to each other.
-
+
Many of the analyses we perform with high-dimensional data relate directly or indirectly to distance. Many clustering and machine learning techniques rely on being able to define distance, using features or predictors. For example, to create _heatmaps_, which are widely used in genomics and other high-throughput fields, a distance is computed explicitly.
-
+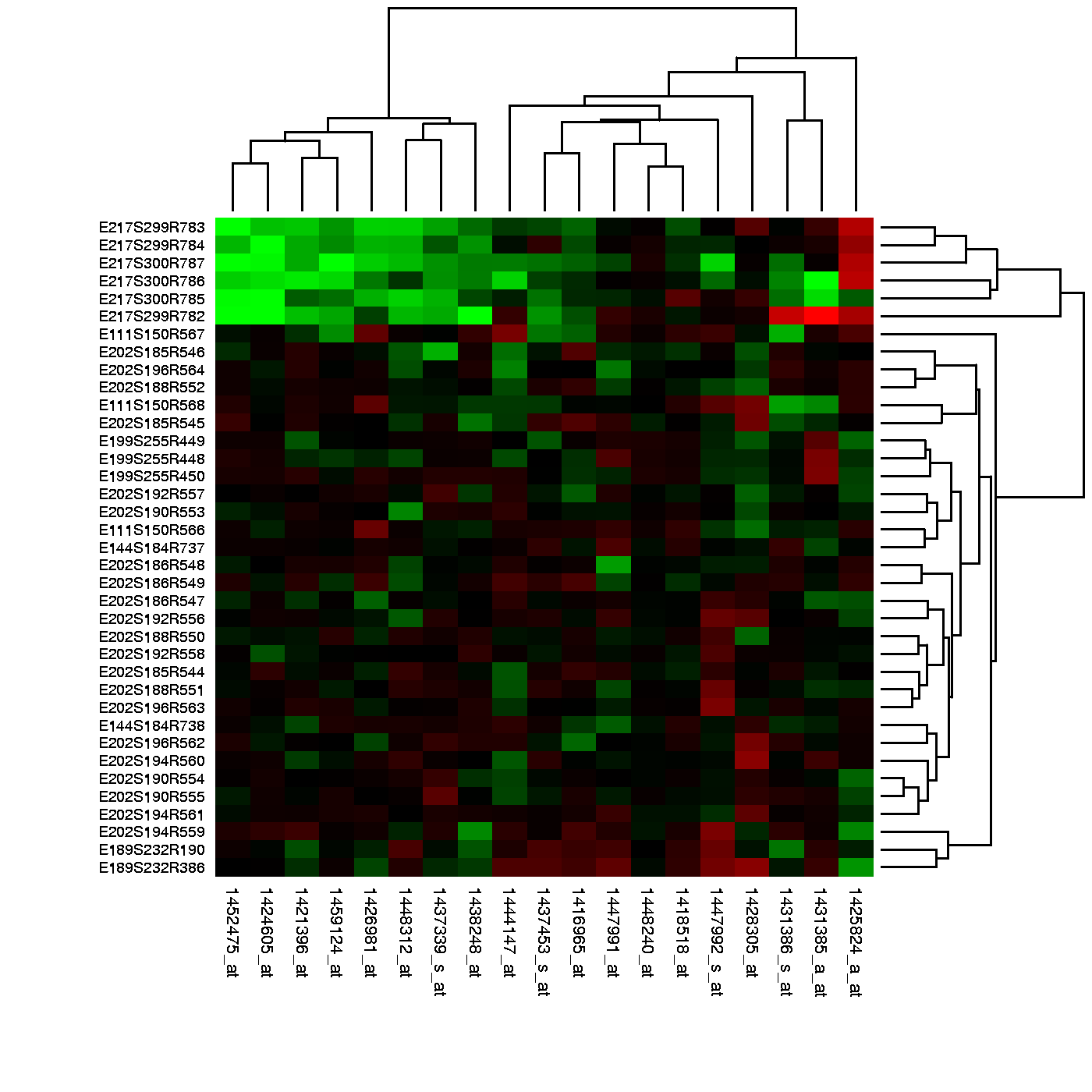
In these plots the measurements, which are stored in a matrix, are
represented with colors after the columns and rows have been
@@ -126,5 +126,3 @@ as.matrix(d)[1,87]
```
It is important to remember that if we run `dist` on `e`, it will compute all pairwise distances between genes. This will try to create a $22215 \times 22215$ matrix that may crash your R sessions.
-
-
diff --git a/modeling/hierarchical_models.Rmd b/modeling/hierarchical_models.Rmd
index 382a41b2..27137ce4 100644
--- a/modeling/hierarchical_models.Rmd
+++ b/modeling/hierarchical_models.Rmd
@@ -10,7 +10,7 @@ opts_chunk$set(fig.path=paste0("figure/", sub("(.*).Rmd","\\1",basename(knitr:::
## Hierarchical Models
-In this section, we use the mathematical theory which describes an approach that has become widely applied in the analysis of high-throughput data. The general idea is to build a _hierachichal model_ with two levels. One level describes variability across samples/units, and the other describes variability across features. This is similar to the baseball example in which the first level described variability across players and the second described the randomness for the success of one player. The first level of variation is accounted for by all the models and approaches we have described here, for example the model that leads to the t-test. The second level provides power by permitting us to "borrow" information from all features to inform the inference performed on each one.
+In this section, we use the mathematical theory which describes an approach that has become widely applied in the analysis of high-throughput data. The general idea is to build a _hierachichal model_ with two levels. One level describes variability across samples/units, and the other describes variability across features. This is similar to the baseball example in which the first level described variability across players and the second described the randomness for the success of one player. The first level of variation is accounted for by all the models and approaches we have described here, for example the model that leads to the t-test. The second level provides power by permitting us to "borrow" information from all features to inform the inference performed on each one.
Here we describe one specific case that is currently the most widely
used approach to inference with gene expression data. It is the model
@@ -20,7 +20,7 @@ adapted to develop methods for other data types such as RNAseq by, for example,
[DESeq2](http://www.ncbi.nlm.nih.gov/pubmed/25516281). This package
provides an alternative to the t-test that greatly improves power by
modeling the variance. While in the baseball example we modeled averages, here we model variances. Modelling variances requires more advanced math, but the concepts are practically the same. We motivate and demonstrate the approach with
-an example.
+an example.
Here is a volcano showing effect sizes and p-value from applying a t-test to data from an experiment running six replicated samples with 16 genes artificially made to be different in two groups of three samples each. These 16 genes are the only genes for which the alternative hypothesis is true. In the plot they are shown in blue.
@@ -47,7 +47,7 @@ We cut-off the range of the y-axis at 4.5, but there is one blue point with a p-
sum( p.adjust(tt$p.value,method = "BH")[spike] < 0.05)
```
-This of course has to do with the low power associated with a sample size of three in each group. The second finding is that if we forget about inference and simply rank the genes based on the size of the t-statistic, we obtain many false positives in any rank list of size larger than 1. For example, six of the top 10 genes ranked by t-statistic are false positives.
+This of course has to do with the low power associated with a sample size of three in each group. The second finding is that if we forget about inference and simply rank the genes based on the size of the t-statistic, we obtain many false positives in any rank list of size larger than 1. For example, six of the top 10 genes ranked by t-statistic are false positives.
```{r}
table( top50=rank(tt$p.value)<= 10, spike) #t-stat and p-val rank is the same
@@ -56,7 +56,7 @@ table( top50=rank(tt$p.value)<= 10, spike) #t-stat and p-val rank is the same
In the plot we notice that these are mostly genes for which the effect size is relatively small, implying that the estimated standard error is small. We can confirm this with a plot:
```{r pval_versus_sd, fig.cap="p-values versus standard deviation estimates."}
-tt$s <- apply(exprs(rma95), 1, function(row)
+tt$s <- apply(exprs(rma95), 1, function(row)
sqrt(.5 * (var(row[1:3]) + var(row[4:6]) ) ) )
with(tt, plot(s, -log10(p.value), cex=.8, pch=16,
log="x",xlab="estimate of standard deviation",
@@ -70,7 +70,7 @@ $$
s^2 \sim s_0^2 F_{d,d_0}
$$
-Because we have thousands of data points, we can actually check this assumption and also estimate the parameters $s_0$ and $d_0$. This particular approach is referred to as empirical Bayes because it can be described as using data (empirical) to build the prior distribution (Bayesian approach).
+Because we have thousands of data points, we can actually check this assumption and also estimate the parameters $s_0$ and $d_0$. This particular approach is referred to as empirical Bayes because it can be described as using data (empirical) to build the prior distribution (Bayesian approach).
Now we apply what we learned with the baseball example to the standard error estimates. As before we have an observed value for each gene $s_g$, a sampling distribution as a prior distribution. We can therefore compute a posterior distribution for the variance $\sigma^2_g$ and obtain the posterior mean. You can see the details of the derivation in [this paper](http://www.ncbi.nlm.nih.gov/pubmed/16646809).
@@ -78,7 +78,7 @@ $$
\mbox{E}[\sigma^2_g \mid s_g] = \frac{d_0 s_0^2 + d s^2_g}{d_0 + d}
$$
-As in the baseball example, the posterior mean _shrinks_ the observed variance $s_g^2$ towards the global variance $s_0^2$ and the weights depend on the sample size through the degrees of freedom $d$ and, in this case, the shape of the prior distribution through $d_0$.
+As in the baseball example, the posterior mean _shrinks_ the observed variance $s_g^2$ towards the global variance $s_0^2$ and the weights depend on the sample size through the degrees of freedom $d$ and, in this case, the shape of the prior distribution through $d_0$.
In the plot above we can see how the variance estimates _shrink_ for 40 genes (code not shown):
@@ -86,7 +86,7 @@ In the plot above we can see how the variance estimates _shrink_ for 40 genes (c
```{r shrinkage, fig.cap="Illustration of how estimates shrink towards the prior expectation. Forty genes spanning the range of values were selected.",message=FALSE, echo=FALSE}
library(limma)
fit <- lmFit(rma95, model.matrix(~ fac))
-ebfit <- ebayes(fit)
+ebfit <- eBayes(fit)
n <- 40
qs <- seq(from=0,to=.2,length=n)
@@ -105,7 +105,7 @@ An important aspect of this adjustment is that genes having a sample standard de
```{r volcano-plot2, message=FALSE, fig.cap="Volcano plot for moderated t-test comparing two groups. Spiked-in genes are denoted with blue. Among the rest of the genes, those with p-value < 0.01 are denoted with red.",message=FALSE}
library(limma)
fit <- lmFit(rma95, model.matrix(~ fac))
-ebfit <- ebayes(fit)
+ebfit <- eBayes(fit)
limmares <- data.frame(dm=coef(fit)[,"fac2"], p.value=ebfit$p.value[,"fac2"])
with(limmares, plot(dm, -log10(p.value),cex=.8, pch=16,
col=cols,xlab="difference in means",
@@ -113,8 +113,8 @@ with(limmares, plot(dm, -log10(p.value),cex=.8, pch=16,
abline(h=2,v=c(-.2,.2), lty=2)
```
-The number of false positives in the top 10 is now reduced to 2.
+The number of false positives in the top 10 is now reduced to 2.
```{r}
-table( top50=rank(limmares$p.value)<= 10, spike)
+table( top50=rank(limmares$p.value)<= 10, spike)
```
diff --git a/modeling/modeling.Rmd b/modeling/modeling.Rmd
index b747dff8..0b522de5 100644
--- a/modeling/modeling.Rmd
+++ b/modeling/modeling.Rmd
@@ -15,9 +15,9 @@ opts_chunk$set(fig.path=paste0("figure/", sub("(.*).Rmd","\\1",basename(knitr:::
When we see a p-value in the literature, it means a probability distribution of some sort was used to quantify the null hypothesis. Many times deciding which probability distribution to use is relatively straightforward. For example, in the tea tasting challenge we can use simple probability calculations to determine the null distribution. Most p-values in the scientific literature are based on sample averages or least squares estimates from a linear model and make use of the CLT to approximate the null distribution of their statistic as normal.
-The CLT is backed by theoretical results that guarantee that the approximation is accurate. However, we cannot always use this approximation, such as when our sample size is too small. Previously, we described how the sample average can be approximated as t-distributed when the population data is approximately normal. However, there is no theoretical backing for this assumption. We are now *modeling*. In the case of height, we know from experience that this turns out to be a very good model.
+The CLT is backed by theoretical results that guarantee that the approximation is accurate. However, we cannot always use this approximation, such as when our sample size is too small. Previously, we described how the sample average can be approximated as t-distributed when the population data is approximately normal. However, there is no theoretical backing for this assumption. We are now *modeling*. In the case of height, we know from experience that this turns out to be a very good model.
-But this does not imply that every dataset we collect will follow a normal distribution. Some examples are: coin tosses, the number of people who win the lottery, and US incomes. The normal distribution is not the only parametric distribution that is available for modeling. Here we provide a very brief introduction to some of the most widely used parametric distributions and some of their uses in the life sciences. We focus on the models and concepts needed to understand the techniques currently used to perform statistical inference on high-throughput data. To do this we also need to introduce the basics of Bayesian statistics. For more in-depth description of probability models and parametric distributions please consult a Statistics textbook such as [this one](https://www.stat.berkeley.edu/~rice/Book3ed/index.html).
+But this does not imply that every dataset we collect will follow a normal distribution. Some examples are: coin tosses, the number of people who win the lottery, and US incomes. The normal distribution is not the only parametric distribution that is available for modeling. Here we provide a very brief introduction to some of the most widely used parametric distributions and some of their uses in the life sciences. We focus on the models and concepts needed to understand the techniques currently used to perform statistical inference on high-throughput data. To do this we also need to introduce the basics of Bayesian statistics. For more in-depth description of probability models and parametric distributions please consult a Statistics textbook such as [this one](https://www.stat.berkeley.edu/~rice/Book3ed/index.html).
## The Binomial Distribution
@@ -29,7 +29,7 @@ $$
with $p$ the probability of success. The best known example is coin tosses with $S$ the number of heads when tossing $N$ coins. In this example $p=0.5$.
-Note that $S/N$ is the average of independent random variables and thus the CLT tells us that $S$ is approximately normal when $N$ is large. This distribution has many applications in the life sciences. Recently, it has been used by the variant callers and genotypers applied to next generation sequencing. A special case of this distribution is approximated by the Poisson distribution which we describe next.
+Note that $S/N$ is the average of independent random variables and thus the CLT tells us that $S$ is approximately normal when $N$ is large. This distribution has many applications in the life sciences. Recently, it has been used by the variant callers and genotypers applied to next generation sequencing. A special case of this distribution is approximated by the Poisson distribution which we describe next.
## The Poisson Distribution
@@ -50,7 +50,7 @@ $$
\mbox{Pr}(S=k)=\frac{\lambda^k \exp{-\lambda}}{k!}
$$
-The Poisson distribution is commonly used in RNA-seq analyses. Because we are sampling thousands of molecules and most genes represent a very small proportion of the totality of molecules, the Poisson distribution seems appropriate.
+The Poisson distribution is commonly used in RNA-seq analyses. Because we are sampling thousands of molecules and most genes represent a very small proportion of the totality of molecules, the Poisson distribution seems appropriate.
So how does this help us? One way is that it provides insight about the statistical properties of summaries that are widely used in practice. For example, let's say we only have one sample from each of a case and control RNA-seq experiment and we want to report the genes with the largest fold-changes. One insight that the Poisson model provides is that under the null hypothesis of no true differences, the statistical variability of this quantity depends on the total abundance of the gene. We can show this mathematically, but here is a quick simulation to demonstrate the point:
@@ -58,7 +58,7 @@ So how does this help us? One way is that it provides insight about the statisti
N=10000##number of genes
lambdas=2^seq(1,16,len=N) ##these are the true abundances of genes
y=rpois(N,lambdas)##note that the null hypothesis is true for all genes
-x=rpois(N,lambdas)
+x=rpois(N,lambdas)
ind=which(y>0 & x>0)##make sure no 0s due to ratio and log
library(rafalib)
@@ -84,7 +84,7 @@ The data is contained in a `SummarizedExperiment` object, which we do not descri
x <- assay(se)[,23]
y <- assay(se)[,24]
ind=which(y>0 & x>0)##make sure no 0s due to ratio and log
-splot((log2(x)+log2(y))/2,log(x/y),subset=ind)
+splot((log2(x)+log2(y))/2,log2(x/y),subset=ind)
```
If we compute the standard deviations across four individuals, it is quite a bit higher than what is predicted by a Poisson model. Assuming most genes are differentially expressed across individuals, then, if the Poisson model is appropriate, there should be a linear relationship in this plot:
@@ -108,9 +108,11 @@ The reason for this is that the variability plotted here includes biological var
To illustrate the concept of maximum likelihood estimates (MLE), we use a relatively simple dataset containing palindrome locations in the HMCV genome. We read in the locations of the palindrome and then count the number of palindromes in each 4,000 basepair segments.
```{r, palindrome_count_histogram, fig.cap="Palindrome count histogram."}
-datadir="http://www.biostat.jhsph.edu/bstcourse/bio751/data"
-x=read.csv(file.path(datadir,"hcmv.csv"))[,2]
+#datadir="http://www.biostat.jhsph.edu/bstcourse/bio751/data"
+#x=read.csv(file.path(datadir,"hcmv.csv"))[,2]
+library(dagdata)
+data(hcmv)
breaks=seq(0,4000*round(max(x)/4000),4000)
tmp=cut(x,breaks)
counts=table(tmp)
@@ -126,7 +128,7 @@ $$
\Pr(X_1=k_1,\dots,X_n=k_n;\lambda) = \prod_{i=1}^n \lambda^{k_i} / k_i! \exp ( -\lambda)
$$
-The MLE is the value of $\lambda$ that maximizes the likelihood:.
+The MLE is the value of $\lambda$ that maximizes the likelihood:.
$$
\mbox{L}(\lambda; X_1=k_1,\dots,X_n=k_1)=\exp\left\{\sum_{i=1}^n \log \Pr(X_i=k_i;\lambda)\right\}
@@ -135,7 +137,7 @@ $$
In practice, it is more convenient to maximize the log-likelihood which is the summation that is exponentiated in the expression above. Below we write code that computes the log-likelihood for any $\lambda$ and use the function `optimize` to find the value that maximizes this function (the MLE). We show a plot of the log-likelihood along with vertical line showing the MLE.
```{r mle, fig.cap="Likelihood versus lambda."}
-l<-function(lambda) sum(dpois(counts,lambda,log=TRUE))
+l<-function(lambda) sum(dpois(counts,lambda,log=TRUE))
lambdas<-seq(3,7,len=100)
ls <- exp(sapply(lambdas,l))
@@ -159,13 +161,13 @@ qqplot(theoretical,counts)
abline(0,1)
```
-We therefore can model the palindrome count data with a Poisson with $\lambda=5.16$.
+We therefore can model the palindrome count data with a Poisson with $\lambda=5.16$.
## Distributions for Positive Continuous Values
Different genes vary differently across biological replicates. Later, in the hierarchical models chapter, we will describe one of the [most influential statistical methods](http://www.ncbi.nlm.nih.gov/pubmed/16646809) in the analysis of genomics data. This method provides great improvements over naive approaches to detecting differentially expressed genes. This is achieved by modeling the distribution of the gene variances. Here we describe the parametric model used in this method.
-We want to model the distribution of the gene-specific standard errors. Are they normal? Keep in mind that we are modeling the population standard errors so CLT does not apply, even though we have thousands of genes.
+We want to model the distribution of the gene-specific standard errors. Are they normal? Keep in mind that we are modeling the population standard errors so CLT does not apply, even though we have thousands of genes.
As an example, we use an experimental data that included both technical and biological replicates for gene expression measurements on mice. We can load the data and compute the gene specific sample standard error for both the technical replicates and the biological replicates
@@ -204,7 +206,7 @@ shist(techsds,unit=0.1,col=2,add=TRUE)
legend("topright",c("Biological","Technical"), col=c(1,2),lty=c(1,1))
```
-An important observation here is that the biological variability is substantially higher than the technical variability. This provides strong evidence that genes do in fact have gene-specific biological variability.
+An important observation here is that the biological variability is substantially higher than the technical variability. This provides strong evidence that genes do in fact have gene-specific biological variability.
If we want to model this variability, we first notice that the normal distribution is not appropriate here since the right tail is rather large. Also, because SDs are strictly positive, there is a limitation to how symmetric this distribution can be.
A qqplot shows this very clearly:
@@ -214,13 +216,13 @@ qqnorm(biosds)
qqline(biosds)
```
-There are parametric distributions that possess these properties (strictly positive and _heavy_ right tails). Two examples are the _gamma_ and _F_ distributions. The density of the gamma distribution is defined by:
+There are parametric distributions that possess these properties (strictly positive and _heavy_ right tails). Two examples are the _gamma_ and _F_ distributions. The density of the gamma distribution is defined by:
$$
f(x;\alpha,\beta)=\frac{\beta^\alpha x^{\alpha-1}\exp{-\beta x}}{\Gamma(\alpha)}
$$
-It is defined by two parameters $\alpha$ and $\beta$ that can, indirectly, control location and scale. They also control the shape of the distribution. For more on this distribution please refer to [this book](https://www.stat.berkeley.edu/~rice/Book3ed/index.html).
+It is defined by two parameters $\alpha$ and $\beta$ that can, indirectly, control location and scale. They also control the shape of the distribution. For more on this distribution please refer to [this book](https://www.stat.berkeley.edu/~rice/Book3ed/index.html).
Two special cases of the gamma distribution are the chi-squared and exponential distribution. We used the chi-squared earlier to analyze a 2x2 table data. For chi-square, we have $\alpha=\nu/2$ and $\beta=2$ with $\nu$ the degrees of freedom. For exponential, we have $\alpha=1$ and $\beta=\lambda$ the rate.
@@ -254,7 +256,7 @@ for(d in c(1,5,10)){
xlab="sd",ylab="density",freq=FALSE,nc=100,xlim=c(0,1))
dd=df(sds^2/s0^2,11,d)
##multiply by normalizing constant to assure same range on plot
- k=sum(tmp$density)/sum(dd)
+ k=sum(tmp$density)/sum(dd)
lines(sds,dd*k,type="l",col=2,lwd=2)
}
}
@@ -283,4 +285,3 @@ dd=df(sds^2/estimates$scale,11,estimates$df2)
k=sum(tmp$density)/sum(dd) ##a normalizing constant to assure same area in plot
lines(sds, dd*k, type="l", col=2, lwd=2)
```
-