Data Structures and Algorithms in JavaScript

This repository covers the implementation of the classical algorithms and data structures in JavaScript.

Usage

You can clone the repo or install the code from NPM:

npm install dsa.js

and then you can import it into your programs or CLI

const { LinkedList, Queue, Stack } = require('dsa.js');

For a full list of all the exposed data structures and algorithms see.

Book

You can check out the dsa.js book that goes deeper into each topic and provide additional illustrations and explanations.

• Algorithmic toolbox to avoid getting stuck while coding.
• Explains data structures similarities and differences.
• Algorithm analysis fundamentals (Big O notation, Time/Space complexity) and examples.
• Time/space complexity cheatsheet.

Data Structures

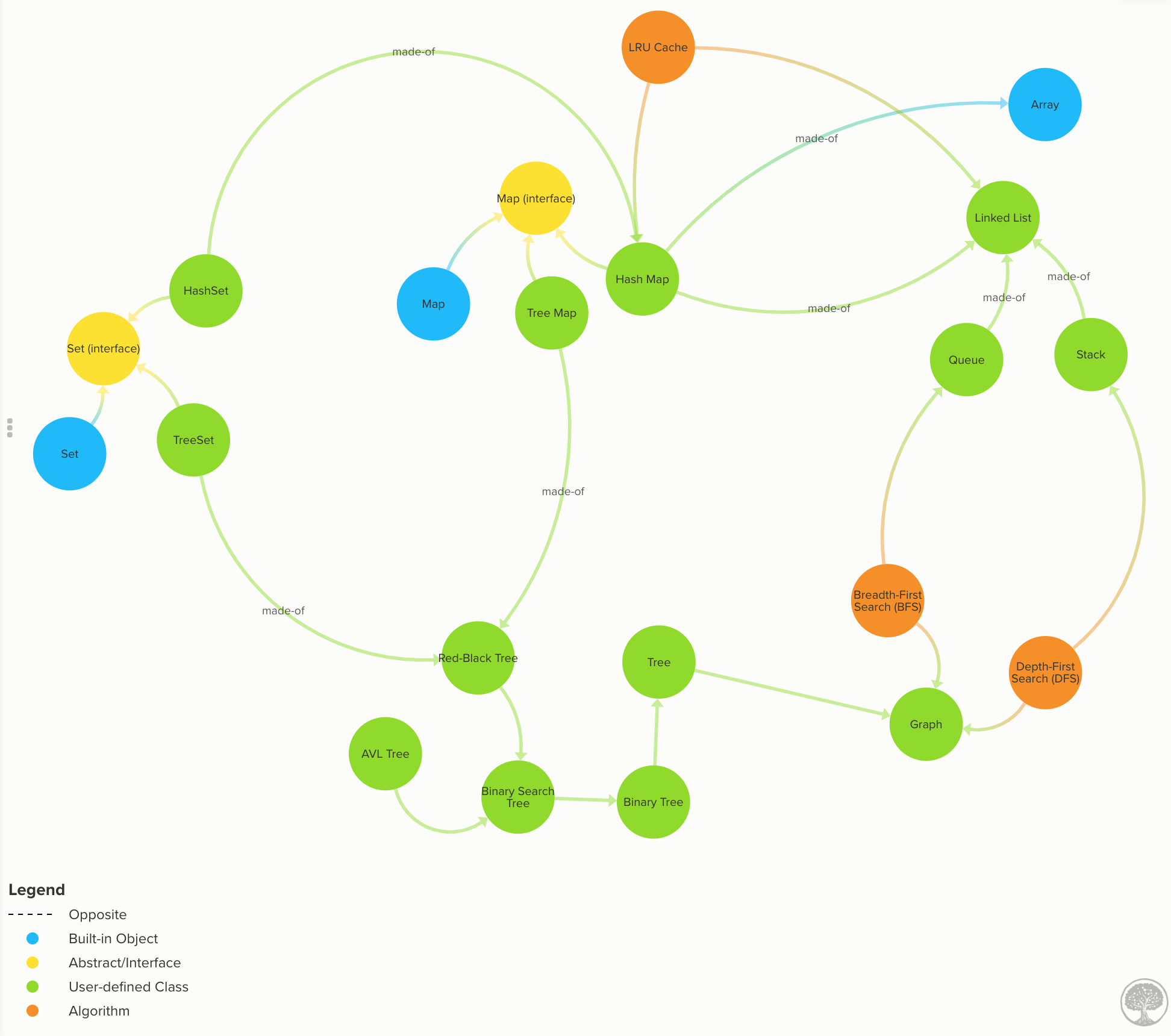
We are covering the following data structures.

Linear Data Structures

1. Arrays: Built-in in most languages so not implemented here. Array Time complexity

2. Linked Lists: each data node has a link to the next (and previous). Code | Linked List Time Complexity

   .

3. Queue: data flows in a "first-in, first-out" (FIFO) manner. Code | Queue Time Complexity

   .

4. Stacks: data flows in a "last-in, first-out" (LIFO) manner. Code | Stack Time Complexity

   .

Non-Linear Data Structures

1. Trees: data nodes has zero or more adjacent nodes a.k.a. children. Each node can only have one parent node otherwise is a graph not a tree. Code | Docs

   1. Binary Trees: same as tree but only can have two children at most. Code | Docs

   2. Binary Search Trees (BST): same as binary tree, but the nodes value keep this order left < parent < rigth. Code | BST Time complexity

   3. AVL Trees: Self-balanced BST to maximize look up time. Code | AVL Tree docs | Self-balancing & tree rotations docs

      .

   4. Red-Black Trees: Self-balanced BST more loose than AVL to maximize insertion speed. Code

2. Maps: key-value store.

   1. Hash Maps: implements map using a hash function. Code | HashMap time complexity

   2. Tree Maps: implement map using a self-balanced BST. Code | TreeMap docs | TreeMap time complexity .

3. Graphs: data nodes that can have a connection or edge to zero or more adjacent nodes. Unlike trees, nodes can have multiple parents, loops. Code | Graph Time Complexity

Algorithms

• Sorting algorithms

  • Bubble Sort. Code | Docs

  • Insertion Sort. Code | Docs

  • Selection Sort. Code | Docs

  • Merge Sort. Code | Docs

  • Quick sort. Code | Docs

• Greedy Algorithms

  • Fractional Knapsack Problem. Code | Docs

• Divide and Conquer

  • Fibonacci Numbers. Code | Docs

• Dynamic Programming

  • Fibonacci with memoization. Code | Docs

• Backtracking algorithms

  • Word permutations. Code | Docs