ccdMPRPenetration() bug, wrong dir penetration depth

[Mikez2015]

Hello.

ccdMPRPenetration() return wrong dir penetration depth.

Please, see this video, bright green stick - it's dir penetration:
https://youtu.be/vN_u3Ig1C2c

I think this is due to this problem: ccdVec3PointTriDist2 computes different distance with / without witness points. #55

Really need help.. I hope the project is not abandoned.

[Mikez2015]

Bug in ccdVec3PointTriDist2

[Mikez2015]

Bug there:

if ((ccdIsZero(s) || s > CCD_ZERO)
            && (ccdEq(s, CCD_ONE) || s < CCD_ONE)
            && (ccdIsZero(t) || t > CCD_ZERO)
            && (ccdEq(t, CCD_ONE) || t < CCD_ONE)
            && (ccdEq(t + s, CCD_ONE) || t + s < CCD_ONE))

If we replace this condition with:
if (1)

issue is solved.

[SeanCurtis-TRI]

Just as a reality check, these are the lines of code to which you are referring, yes?

https://github.com/danfis/libccd/blob/master/src/vec3.c#L176-L180

The solution will have to be more nuanced than just setting that entire branch of logic to true. :) That block code only works if the query point projects onto the triangle and shouldn't be exercised unless that's true. I can imagine in your case it seems to work because the point in questions is positioned right at the threshold of successfully projecting.

The true bug is going to be more subtle. It's going to be related to the tolerances built into the successful projection test and what happens in the alternate branch when that threshold is crossed. Ideally, the two branches should, at the limit, produce the same answer as we approach the threshold; but they are apparently not doing so.

Looking at your video, I hypothesize that what we're seeing is that when the "has projected" test fails and we evaluate the distance from the point P to the nearest point on each triangle edge Qi, the closest pair (P, Qi)'s distance is essentially epsilon in length which means the direction of the vector between them is largely defined by rounding error.

Ultimately, if you could provide some code that reproduces this (as done in the issue you linked to), it would aid considerably in resolving this. (Although, it clearly increases the burden on you, it definitely increases the likelihood of the issue being addressed).

[Mikez2015]

Just as a reality check, these are the lines of code to which you are referring, yes?
Yes these lines

The solution will have to be more nuanced than just setting that entire branch of logic to true. :) That block code only works if the query point projects onto the triangle and shouldn't be exercised unless that's true. I can imagine in your case it seems to work because the point in questions is positioned right at the threshold of successfully projecting.

The true bug is going to be more subtle. It's going to be related to the tolerances built into the successful projection test and what happens in the alternate branch when that threshold is crossed. Ideally, the two branches should, at the limit, produce the same answer as we approach the threshold; but they are apparently not doing so.

I understand that this is not the best solution, but I needed at least some solution that would work. I was also surprised that it works, but it is. I checked on different models - boxes, cylinders, pyramids, moved them from different sides and from different angles, this is my strange solution that really works well. I saw some problems with the direction of the penetration vector only when using spheres.
Of course, I would like to know a truly mathematically correct solution, and not such as mine. But I'm not good at geometry.

Looking at your video, I hypothesize that what we're seeing is that when the "has projected" test fails and we evaluate the distance from the point P to the nearest point on each triangle edge Qi, the closest pair (P, Qi)'s distance is essentially epsilon in length which means the direction of the vector between them is largely defined by rounding error.

I also think that this is due to calculation errors, but it is definitely not related to float precision, since I tried the option with double too.
Unfortunately, to fix the ccdVec3PointTriDist2 function myself, I do not have enough knowledge of geometry.

Ultimately, if you could provide some code that reproduces this (as done in the issue you linked to), it would aid considerably in resolving this. (Although, it clearly increases the burden on you, it definitely increases the likelihood of the issue being addressed).

Which part of the code do you mean? You won’t read thousands of lines of code. I am completely sure that the problem is in the ccdVec3PointTriDist2 function, which is called from the findPenetr function, which is called from the ccdMPRPenetration function. Most likely the problem is exactly what you wrote "I hypothesize that what we're seeing is that when the" has projected "test fails and we evaluate the distance from the point P to the nearest point on each triangle edge Qi, the closest pair (P, Qi) 's distance is essentially epsilon in length which means the direction of the vector between them is largely defined by rounding error. " This is the only logical reason for the error.
I would be very grateful if you could help fix this, like many other libccd users.

[SeanCurtis-TRI]

I checked on different models

You'd have to check various configurations as well. You could change numerous models and not run into the situation where this change would explode if you just don't configure them correctly.

it is definitely not related to float precision

I didn't say it was related to "float precision". I said it was related to tolerances. You'll note that ccdIsZero actually tests the absolute value of the quantity under test against an epsilon. That epsilon value tends to scale with the precision available. But it's still a tolerance and that can lead to funny artifacts if your two branches don't have proper continuity.

One of the factors that is important, from a geometry sense, is the scale of the problem. The default epsilon value works best when all of the parameters are approximately unit magnitude. Ultimately, epsilon should really scale with respect to the size of the problem (otherwise, for large triangles, the absolute value of epsilon falls below rounding error, and for small triangles, the absolute value becomes a larger portion of the valid numerical space).

I agree with you, the complete diagnosis of the code is complex. And the solution more so. I hadn't intended to suggest you should implement the solution. I was merely documenting why your apparent solution is not a general solution that could/should be included in a PR. Resolving what appears to be a very real bug is going to be more complex than just setting the test to true.

Which part of the code do you mean?

I mean a piece of reproducible code that would allow someone who has no access to your code base the ability to see the bug. That would the single greatest contribution contained in this issue. It makes the bug definitive and empowers someone to address it.

In an ideal world, you should be able to reproduce this in just a few lines of code.

• Configure a triangle
• Select a point
• Call ccdVec3PointTriDist2
• perturb the point by a small amount (epsilon)
• Call ccdVec3PointTriDist2 again and show that the result jumps discontinuously.

The challenge is finding the triangle and point that is causing you problems because it is, ultimately, being generated inside libccd. Still, build enough things in debug build and you should be able to capture those parameters.

[Mikez2015]

The challenge is finding the triangle and point that is causing you problems because it is, ultimately, being generated inside libccd. Still, build enough things in debug build and you should be able to capture those parameters.

Thx a lot, I will try it.
I will continue to fight this error and write the process here.

[Mikez2015]

ccdVec3PointTriDist2

The function incorrectly considers the distance from the zero point to the triangle with the following coordinates:

A(1.650970, -0.102323, -2.994949);
B(-1.613953, -0.102323, 2.534958);
C(-1.613953, -0.102323, -2.994949);

The function returns the distance to the triangle equal to 0.143770, but the correct distance is 0.102323.

A couple of pictures for clarity:

I myself will continue to search for errors in this function, but I will be grateful for any help.

[Mikez2015]

One of the factors that is important, from a geometry sense, is the scale of the problem. The default epsilon value works best when all of the parameters are approximately unit magnitude. Ultimately, epsilon should really scale with respect to the size of the problem (otherwise, for large triangles, the absolute value of epsilon falls below rounding error, and for small triangles, the absolute value becomes a larger portion of the valid numerical space).

I tried to change the value of CCD_EPS in different directions and in different orders, but this did not produce any result.

[Mikez2015]

I began to research this comparison on the correctness of work:
https://github.com/danfis/libccd/blob/master/src/vec3.c#L176-L180

I found out that if the function does not work properly, the condition is not met
(ccdIsZero(t) || t > CCD_ZERO)
, because the variable "t" becomes negative.

Is it possible that a variable "t" is being calculated incorrectly?
https://github.com/danfis/libccd/blob/master/src/vec3.c#L173

[SeanCurtis-TRI]

This is a great effort; you've got the right idea.

However, I've looked at your example and I think you have an error. Here's the scenario you've created:

• Two triangles, lying on the y = -0.102323 plane.
• The query point is the origin (0, 0, 0).
• The distance from origin to triangle is 0.102323 if and only if the origin's projection onto the y = -0.10232 plane lies inside the triangle.

         +z
         ^
         ┆
    B    ┆
    │ ╲  ┆O
┄┄┄┄┄┄┄┄╲┼┄┄┄┄┄┄┄┄┄┄┄> +x
    │    ┆╲
    │    ┆  ╲
    C────┆────A
         ┆

Figure 1: "Bad" triangle drawn on the y = -0.102323 plane. The picture is merely illustrative showing the relative position of the triangle vertices.

For the "erroneous" triangle, you assume the correct distance is 0.102323 which implies the origin projects to a point inside the second triangle. However, that appears not to be the case. Consider the vector from A to B (AB). To be inside the triangle, the vector from A to O (AO) must lie on AB's "left" side. By my calculations, it doesn't. Here's some python code to illustrate that.

import numpy as np
def det(a, b):
  return a[0] * b[1] - a[1] * b[0]
# We're going to turn this into a 2D problem; because the y-value doesn't matter
# for testing the *projection* of the origin on the y = -0.102323 plane.
A = np.array((1.650970, -2.994949))
B = np.array((-1.613953, 2.534958))
p_AB = B - A
p_AO = -A
# for origin to project onto the triangle, this value must be <= 0.
det(p_AO, p_AB)
# evaluates to 0.6485673141370007

In fact, if I take this a step further, the projection of the origin lies 0.100994 units outside the triangle. And that means the origin is 0.14377027 units away from the triangle.

Unfortunately, this means the "error" condition isn't really an error condition. We'll have to keep digging.

[Mikez2015]

For the "erroneous" triangle, you assume the correct distance is 0.102323 which implies the origin projects to a point inside the second triangle. However, that appears not to be the case.

Stop, sorry, I'm a little confused. Let us take one moment to uttle. I correctly understood that you are claiming that the point
P (0,0)
does not belong to the triangle

A(1.650970,-2.994949);
B(-1.613953,  2.534958);
C(-1.613953,  -2.994949);

?

[SeanCurtis-TRI]

I was worried that might be a bit opaque. Sorry about that. I'm happy to walk through it.

I correctly understood that you are claiming that the point P (0,0) does not belong to the triangle

Correct. Everything else in the message was about showing that to be the case.

[Mikez2015]

I was worried that might be a bit opaque. Sorry about that. I'm happy to walk through it.

I correctly understood that you are claiming that the point P (0,0) does not belong to the triangle

Correct. Everything else in the message was about showing that to be the case.

The function ccdVec3PointTriDist2 thinks it belongs. I have to double-check this with another simple algorithm. Thanks for the help, I will write about the result later.

[Mikez2015]

Correct. Everything else in the message was about showing that to be the case.

I double-checked, you are absolutely right.
Then it turns out that the issue is that the function ccdVec3PointTriDist2 incorrectly determines whether the point belongs to the triangle.

So the error is at the beginning of the function, in this range:

https://github.com/danfis/libccd/blob/master/src/vec3.c#L142-L180

[SeanCurtis-TRI]

the function ccdVec3PointTriDist2 incorrectly determines whether the point belongs to the triangle.

Are you sure about that? It's reporting the correct distance. It seems highly unlikely that it can simultaneously classify it as projecting onto the triangle and compute the correct distance. Admittedly, I haven't run the code to analyze what it's doing. But, I'd be quite surprised if both can happen at the same time.

For the record, a few questions:

• Are you invoking ccdVec3PointTriDist2 with or without witnesses?
• What is your type of ccd_real_t? Double or float?

[Mikez2015]

Are you sure about that? It's reporting the correct distance. It seems highly unlikely that it can simultaneously classify it as projecting onto the triangle and compute the correct distance. Admittedly, I haven't run the code to analyze what it's doing. But, I'd be quite surprised if both can happen at the same time.

Oh, it seems I'm a little confused. Sorry, I didn’t get enough sleep today.
It turns out the opposite, in the previous message I was mistaken.

[Mikez2015]

Are you sure about that? It's reporting the correct distance. It seems highly unlikely that it can simultaneously classify it as projecting onto the triangle and compute the correct distance. Admittedly, I haven't run the code to analyze what it's doing. But, I'd be quite surprised if both can happen at the same time.

You are right again, I was mistaken. Then it turns out that the issue is in these lines:

https://github.com/danfis/libccd/blob/master/src/vec3.c#L198-L214

[Mikez2015]

• Are you invoking ccdVec3PointTriDist2 with or without witnesses?

• What is your type of ccd_real_t? Double or float?

With witnesses... probably witness is not equal to zero..
I tryed both.

[Mikez2015]

Are you sure about that? It's reporting the correct distance. It seems highly unlikely that it can simultaneously classify it as projecting onto the triangle and compute the correct distance. Admittedly, I haven't run the code to analyze what it's doing. But, I'd be quite surprised if both can happen at the same time.

Thank you very much, you helped me a lot in my search. Now I started to suspect a function __ccdVec3PointSegmentDist2.
I will continue to search

[SeanCurtis-TRI]

I'm glad to help. And I'm impressed with how you're tackling this. It might be worth taking a step back and make sure we're investigating the right thing.

As I look at the original post and the video, what we're seeing is a fluctuation in penetration direction. Right now you're focused on penetration depth. It's distinctly possible that even as the direction vector in your video fluctuates discontinuously, you're still getting reasonably continuous depth measurements. So, focusing exclusively on depth may take you down the wrong path.

So, we might need to revisit the core issue with the following questions:

• Where does the direction vector that is being visualized come from?
• What is its relationship to the function in question?
  • I assume, in order for ccdVec3PointTriDist2 to contribute to the direction, then witness must be provided in the call.
• How do we know it's attributable to ccdVec3PointTriDist2?

[Mikez2015]

* Where does the direction vector that is being visualized come from?

My program takes a visualized direction vector from "dir":

int ccdMPRPenetration(const void *obj1, const void *obj2, const ccd_t *ccd,
                      ccd_real_t *depth, ccd_vec3_t *dir, ccd_vec3_t *pos)

libccd/src/mpr.c

Line 117 in 7931e76

int ccdMPRPenetration(const void *obj1, const void *obj2, const ccd_t *ccd,

ccdMPRPenetration takes "dir" vector from "dir":

findPenetr(obj1, obj2, ccd, &portal, depth, dir, pos);

libccd/src/mpr.c

Line 144 in 7931e76

findPenetr(obj1, obj2, ccd, &portal, depth, dir, pos);

findPenetr  takes "dir" vector from "pdir":

        *depth = ccdVec3PointTriDist2(ccd_vec3_origin,
            &ccdSimplexPoint(portal, 1)->v,
            &ccdSimplexPoint(portal, 2)->v,
            &ccdSimplexPoint(portal, 3)->v,
            pdir);

https://github.com/danfis/libccd/blob/7931e764a19ef6b21b443376c699bbc9c6d4fba8/src/mpr.c#L325

ccdVec3PointTriDist2 takes "pdir" vector from "witness":

ccd_real_t ccdVec3PointTriDist2(const ccd_vec3_t *P,
const ccd_vec3_t *x0, const ccd_vec3_t *B,
const ccd_vec3_t *C,
ccd_vec3_t *witness)

https://github.com/danfis/libccd/blob/7931e764a19ef6b21b443376c699bbc9c6d4fba8/src/vec3.c#L137

• What is its relationship to the function in question?

  • I assume, in order for ccdVec3PointTriDist2 to contribute to the direction, then witness must be provided in the call.

• How do we know it's attributable to ccdVec3PointTriDist2?

Please look at this:

I added "printf" to ccdVec3PointTriDist2 to get the information here in this place:

libccd/src/vec3.c

Lines 198 to 201 in 7931e76

	}else{
	dist = __ccdVec3PointSegmentDist2(P, x0, B, witness);
	dist2 = __ccdVec3PointSegmentDist2(P, x0, C, &witness2);

    }else{
    printf("A.X: %f \n", x0->v[0]);
    printf("A.Y: %f \n", x0->v[1]);
    printf("A.Z: %f \n", x0->v[2]);

    printf("B.X: %f \n", B->v[0]);
    printf("B.Y: %f \n", B->v[1]);
    printf("B.Z: %f \n", B->v[2]);

    printf("P.X: %f \n", P->v[0]);
    printf("P.Y: %f \n", P->v[1]);
    printf("P.Z: %f \n", P->v[2]);

    dist = __ccdVec3PointSegmentDist2(P, x0, B, witness);

    printf("dist A B: %f \n", CCD_SQRT(dist));

I got these numbers in the console:

They show that the distance between segment AB and the zero point is 0.143770.
But in fact, this distance should equal or be slightly larger than 0.102323, this can be seen from this picture:

And the distance returned by the function ccdVec3PointSegmentDist2 is almost one and a half times greater, how can this be if the function ccdVec3PointSegmentDist2 works correctly?

Therefore, I conclude that the function ccdVec3PointSegmentDist2 returns the wrong distance.

Maybe I’ve made a mistake again somewhere, if you see where, please show a mistake in the reasoning.

PS:
If you can, calculate in your way the distance from point P (0,0,0)
to segment
A (1.650970, -0.102323, -2.994949)
B (-1.613953, -0.102323, 2.534958).

I am very interested to know what distance you will get.

PSS:
For more information, I additionally printed the value of "witness":

[Mikez2015]

Strange, I checked with another algorithm, and it turned out that ccdVec3PointSegmentDist2 returns the correct value.
Now I'm at a dead end.

[Mikez2015]

Another video with the same problem, now a box-box for simplicity, with depth printing and normal penetration.
It is amazing how such a issue was not noticed at the very beginning.

https://youtu.be/JYF-Bp0NTlU

[SeanCurtis-TRI]

Here's my suggestion for tracking down this bug:

1. Given the second video you produced, we know that the penetration direction should be vertical.
2. In your program, examine the penetration direction, if it's ever not vertical, remember the relative configuration of the two geometries. This will serve as the starting point.
3. Position the two geometries as you've stored it and confirm that when you perform a single query, that the normal is still skewed (we want to make sure there's no history/hidden state involved).
4. Now put print statements everywhere. We know the final calculation is producing a normal in a bad direction, but we don't know where that started, so, ideally, we should examine all of the triangle queries in the sequence.

[Mikez2015]

I am very grateful to you that you continue to help me. Your help is very much needed.

Here's my suggestion for tracking down this bug:

1. Given the second video you produced, we know that the penetration direction should be vertical.

2. In your program, examine the penetration direction, if it's ever not vertical, remember the relative configuration of the two geometries. This will serve as the starting point.

Already done.

3\. Position the two geometries as you've stored it and confirm that when you perform a single query, that the normal is still skewed (we want to make sure there's no history/hidden state involved).

Ок. I think this code will provide it:

		ccd_real_t depth = 0;
		ccd_vec3_t dir, posGlobal;

		dir.v[0] = 0.0f;
		dir.v[1] = 0.0f;
		dir.v[2] = 0.0f;

		int res = ccdMPRPenetration(&ccd1, &ccd2, &ccd, &depth, &dir, &posGlobal);

		std::cout << "dir.x: " << dir.v[0] << std::endl;
		std::cout << "dir.y: " << dir.v[1] << std::endl;
		std::cout << "dir.z: " << dir.v[2] << std::endl;

		exit(0);

4\. Now put print statements _everywhere_. We know the final calculation is producing a normal in a bad direction, but we don't know where that _started_, so, ideally, we should examine all of the triangle queries in the sequence.

I'll do it, but it'll probably take two or three days.

I added some data visualization. Now the portal is drawn with red lines. The yellow triangle is the same ABC triangle to which we are looking for the distance from the zero point.

libccd/src/mpr.c

Lines 325 to 329 in 7931e76

	*depth = ccdVec3PointTriDist2(ccd_vec3_origin,
	&ccdSimplexPoint(portal, 1)->v,
	&ccdSimplexPoint(portal, 2)->v,
	&ccdSimplexPoint(portal, 3)->v,
	pdir);

Zero point - small red sphere, contact position. In this video, the top box barely touches the bottom one, the penetration depth is almost zero.
Please watch this video and give your opinion:

https://youtu.be/f_AP5t7xvyA

[SeanCurtis-TRI]

The new visualization is wonderful! You can see the bad behavior is right on the very edge of the triangle. That suggests to me that it's related to the tolerance and we end up in a branch where the assumption is incorrect by the amount of the tolerance. I'll think about it.

[Mikez2015]

The new visualization is wonderful! You can see the bad behavior is right on the very edge of the triangle. That suggests to me that it's related to the tolerance and we end up in a branch where the assumption is incorrect by the amount of the tolerance. I'll think about it.

I will think about it too. And tomorrow I will print all values penetration normal (pdir, witness) throughout the function.

[sherm1]

Wow! That's an amazing visualization of MPR!

[Mikez2015]

The new visualization is wonderful!

Wow! That's an amazing visualization of MPR!

Thank you, I'm glad you liked it. :)

[Mikez2015]

4\. Now put print statements _everywhere_. We know the final calculation is producing a normal in a bad direction, but we don't know where that _started_, so, ideally, we should examine all of the triangle queries in the sequence.

I have traced how all the variables change that can affect the calculation of the normal vector. I am assuming the portal is building correctly and the problem is not with the portal. In the screenshots, the values are written in red opposite the lines.

Part1 : ==========================================================================

libccd/src/mpr.c

Lines 308 to 329 in 7931e76

	static void findPenetr(const void *obj1, const void *obj2, const ccd_t *ccd,
	ccd_simplex_t *portal,
	ccd_real_t *depth, ccd_vec3_t *pdir, ccd_vec3_t *pos)
	{
	ccd_vec3_t dir;
	ccd_support_t v4;
	unsigned long iterations;
	iterations = 0UL;
	while (1){
	// compute portal direction and obtain next support point
	portalDir(portal, &dir);
	__ccdSupport(obj1, obj2, &dir, ccd, &v4);
	// reached tolerance -> find penetration info
	if (portalReachTolerance(portal, &v4, &dir, ccd)
	|| iterations > ccd->max_iterations){
	*depth = ccdVec3PointTriDist2(ccd_vec3_origin,
	&ccdSimplexPoint(portal, 1)->v,
	&ccdSimplexPoint(portal, 2)->v,
	&ccdSimplexPoint(portal, 3)->v,
	pdir);

Part2 : ==========================================================================

libccd/src/vec3.c

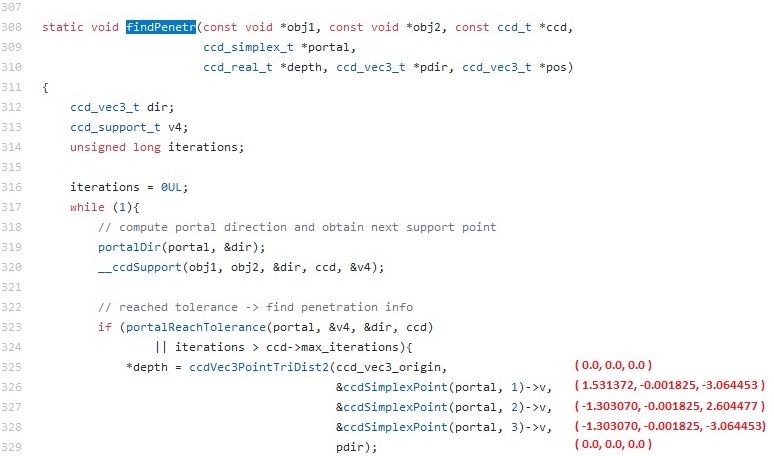
Lines 137 to 165 in 7931e76

	ccd_real_t ccdVec3PointTriDist2(const ccd_vec3_t *P,
	const ccd_vec3_t *x0, const ccd_vec3_t *B,
	const ccd_vec3_t *C,
	ccd_vec3_t *witness)
	{
	// Computation comes from analytic expression for triangle (x0, B, C)
	// T(s, t) = x0 + s.d1 + t.d2, where d1 = B - x0 and d2 = C - x0 and
	// Then equation for distance is:
	// D(s, t) = | T(s, t) - P |^2
	// This leads to minimization of quadratic function of two variables.
	// The solution from is taken only if s is between 0 and 1, t is
	// between 0 and 1 and t + s < 1, otherwise distance from segment is
	// computed.
	ccd_vec3_t d1, d2, a;
	ccd_real_t u, v, w, p, q, r, d;
	ccd_real_t s, t, dist, dist2;
	ccd_vec3_t witness2;
	ccdVec3Sub2(&d1, B, x0);
	ccdVec3Sub2(&d2, C, x0);
	ccdVec3Sub2(&a, x0, P);
	u = ccdVec3Dot(&a, &a);
	v = ccdVec3Dot(&d1, &d1);
	w = ccdVec3Dot(&d2, &d2);
	p = ccdVec3Dot(&a, &d1);
	q = ccdVec3Dot(&a, &d2);
	r = ccdVec3Dot(&d1, &d2);

Part3 : ==========================================================================

libccd/src/vec3.c

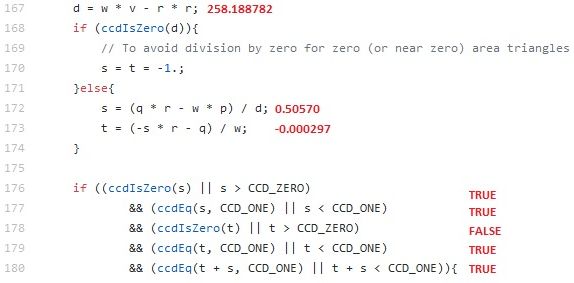
Lines 167 to 180 in 7931e76

	d = w * v - r * r;
	if (ccdIsZero(d)){
	// To avoid division by zero for zero (or near zero) area triangles
	s = t = -1.;
	}else{
	s = (q * r - w * p) / d;
	t = (-s * r - q) / w;
	}
	if ((ccdIsZero(s) || s > CCD_ZERO)
	&& (ccdEq(s, CCD_ONE) || s < CCD_ONE)
	&& (ccdIsZero(t) || t > CCD_ZERO)
	&& (ccdEq(t, CCD_ONE) || t < CCD_ONE)
	&& (ccdEq(t + s, CCD_ONE) || t + s < CCD_ONE)){

Part4 : ==========================================================================

libccd/src/vec3.c

Lines 73 to 128 in 7931e76

	_ccd_inline ccd_real_t __ccdVec3PointSegmentDist2(const ccd_vec3_t *P,
	const ccd_vec3_t *x0,
	const ccd_vec3_t *b,
	ccd_vec3_t *witness)
	{
	// The computation comes from solving equation of segment:
	// S(t) = x0 + t.d
	// where - x0 is initial point of segment
	// - d is direction of segment from x0 (|d| > 0)
	// - t belongs to <0, 1> interval
	//
	// Than, distance from a segment to some point P can be expressed:
	// D(t) = |x0 + t.d - P|^2
	// which is distance from any point on segment. Minimization
	// of this function brings distance from P to segment.
	// Minimization of D(t) leads to simple quadratic equation that's
	// solving is straightforward.
	//
	// Bonus of this method is witness point for free.
	ccd_real_t dist, t;
	ccd_vec3_t d, a;
	// direction of segment
	ccdVec3Sub2(&d, b, x0);
	// precompute vector from P to x0
	ccdVec3Sub2(&a, x0, P);
	t = -CCD_REAL(1.) * ccdVec3Dot(&a, &d);
	t /= ccdVec3Len2(&d);
	if (t < CCD_ZERO || ccdIsZero(t)){
	dist = ccdVec3Dist2(x0, P);
	if (witness)
	ccdVec3Copy(witness, x0);
	}else if (t > CCD_ONE || ccdEq(t, CCD_ONE)){
	dist = ccdVec3Dist2(b, P);
	if (witness)
	ccdVec3Copy(witness, b);
	}else{
	if (witness){
	ccdVec3Copy(witness, &d);
	ccdVec3Scale(witness, t);
	ccdVec3Add(witness, x0);
	dist = ccdVec3Dist2(witness, P);
	}else{
	// recycling variables
	ccdVec3Scale(&d, t);
	ccdVec3Add(&d, &a);
	dist = ccdVec3Len2(&d);
	}
	}
	return dist;
	}

We found out that the projection of the zero point belongs to the triangle is considered correct. It turns out that the function ccdVec3PointSegmentDist2 incorrectly calculates the penetration vector? Or not?

I suppose a good solution is to make it so that when a point lies on an edge of a triangle, the function thinks that it belongs to the triangle. But I can't do it. I also suspect that if you do this, there will be problems in other places.

[SeanCurtis-TRI]

This is sterling work.

I'm going to go over the data/values you've got here. I'd like to confirm that you ran this calculations with 32-bit floats, yes?

[Mikez2015]

This is sterling work.

I'm going to go over the data/values you've got here. I'd like to confirm that you ran this calculations with 32-bit floats, yes?

Yes, 32-bit float.

[Mikez2015]

I'm going to go over the data/values you've got here. I'd like to confirm that you ran this calculations with 32-bit floats, yes?

I suspect that all such isssues happen when the triangle is rectangular and the point touches its hypotenuse.

[SeanCurtis-TRI]

I'd generalize the statement a bit more. Essentially, it's when the MPR evaluation gets very close to an edge. If the edge were axis-aligned, it would be unlikely to cause problems. But as it runs across the axes, you're more likely to encounter rounding error that can mis-classify inside/outside. In other words, it need not be a right triangle.

I have a new hypothesis watching your video. This is based on my rusty mental model of the MPR algorithm. Essentially, we're looking for the triangle through which we can see the origin. If the origin isn't visible through the portal (aka project onto the triangle) we "refine" the portal. Once we've picked the portal, we then do some further calculations. It could be that the code that decides if we have the "right" portal has different tolerances (and critical numerical boundaries) than the subsequent distance calculation. Specifically, the portal classifier can think it's inside a triangle but when doing the actual math, we're not. Being slightly outside of the portal would give us those normal deviations you're experience just at the moment when you're crossing a portal boundary.

[Mikez2015]

I'd generalize the statement a bit more. Essentially, it's when the MPR evaluation gets very close to an edge. If the edge were axis-aligned, it would be unlikely to cause problems. But as it runs across the axes, you're more likely to encounter rounding error that can mis-classify inside/outside. In other words, it need not be a right triangle.

I have a new hypothesis watching your video. This is based on my rusty mental model of the MPR algorithm. Essentially, we're looking for the triangle through which we can see the origin. If the origin isn't visible through the portal (aka project onto the triangle) we "refine" the portal. Once we've picked the portal, we then do some further calculations. It could be that the code that decides if we have the "right" portal has different tolerances (and critical numerical boundaries) than the subsequent distance calculation. Specifically, the portal classifier can think it's inside a triangle but when doing the actual math, we're not. Being slightly outside of the portal would give us those normal deviations you're experience just at the moment when you're crossing a portal boundary.

I thought about all this and decided that the best way is to always assume that the penetration vector coincides with the normal of the triangle. This is almost always the case, except in cases of smooth shapes such as a sphere, then the triangle becomes a point and problems arise. But for a sphere, we can easily find the normal vector of penetration ourselves, knowing the position of the center of the sphere and the point of penetration.
If you can think of a better solution, please write here.

[Mikez2015]

I'd generalize the statement a bit more. Essentially, it's when the MPR evaluation gets very close to an edge. If the edge were axis-aligned, it would be unlikely to cause problems. But as it runs across the axes, you're more likely to encounter rounding error that can mis-classify inside/outside. In other words, it need not be a right triangle.
I have a new hypothesis watching your video. This is based on my rusty mental model of the MPR algorithm. Essentially, we're looking for the triangle through which we can see the origin. If the origin isn't visible through the portal (aka project onto the triangle) we "refine" the portal. Once we've picked the portal, we then do some further calculations. It could be that the code that decides if we have the "right" portal has different tolerances (and critical numerical boundaries) than the subsequent distance calculation. Specifically, the portal classifier can think it's inside a triangle but when doing the actual math, we're not. Being slightly outside of the portal would give us those normal deviations you're experience just at the moment when you're crossing a portal boundary.

I thought about all this and decided that the best way is to always assume that the penetration vector coincides with the normal of the triangle. This is almost always the case, except in cases of smooth shapes such as a sphere, then the triangle becomes a point (the portal becomes a segment) and problems arise. But for a sphere, we can easily find the normal vector of penetration ourselves, knowing the position of the center of the sphere and the point of penetration.
If you can think of a better solution, please write here.