JavaScript 浮点数陷阱及解法

[camsong]

原发于知乎专栏：https://zhuanlan.zhihu.com/ne-fe

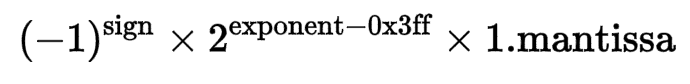
众所周知，JavaScript 浮点数运算时经常遇到会 0.000000001 和 0.999999999 这样奇怪的结果，如 0.1+0.2=0.30000000000000004、1-0.9=0.09999999999999998，很多人知道这是浮点数误差问题，但具体就说不清楚了。本文帮你理清这背后的原理以及解决方案，还会向你解释JS中的大数危机和四则运算中会遇到的坑。

浮点数的存储

首先要搞清楚 JavaScript 如何存储小数。和其它语言如 Java 和 Python 不同，JavaScript 中所有数字包括整数和小数都只有一种类型 — Number。它的实现遵循 IEEE 754 标准，使用 64 位固定长度来表示，也就是标准的 double 双精度浮点数（相关的还有float 32位单精度）。计算机组成原理中有过详细介绍，如果你不记得也没关系。

这样的存储结构优点是可以归一化处理整数和小数，节省存储空间。

64位比特又可分为三个部分：

• 符号位S：第 1 位是正负数符号位（sign），0代表正数，1代表负数
• 指数位E：中间的 11 位存储指数（exponent），用来表示次方数
• 尾数位M：最后的 52 位是尾数（mantissa），超出的部分自动进一舍零



实际数字就可以用以下公式来计算：


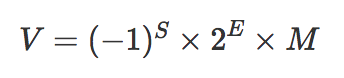
注意以上的公式遵循科学计数法的规范，在十进制是为0<M<10，到二进行就是0<M<2。也就是说整数部分只能是1，所以可以被舍去，只保留后面的小数部分。如 4.5 转换成二进制就是 100.1，科学计数法表示是 1.001*2^2，舍去1后 M = 001。E是一个无符号整数，因为长度是11位，取值范围是 0~2047。但是科学计数法中的指数是可以为负数的，所以再减去一个中间数 1023，[0,1022]表示为负，[1024,2047] 表示为正。如4.5 的指数E = 1025，尾数M为 001。

最终的公式变成：

所以 4.5 最终表示为（M=001、E=1025）：


(图片由此生成 http://www.binaryconvert.com/convert_double.html)

下面再以 0.1 例解释浮点误差的原因， 0.1 转成二进制表示为 0.0001100110011001100(1100循环)，1.100110011001100x2^-4，所以 E=-4+1023=1019；M 舍去首位的1，得到 100110011...。最终就是：


转化成十进制后为 0.100000000000000005551115123126，因此就出现了浮点误差。

为什么 0.1+0.2=0.30000000000000004？

计算步骤为：

// 0.1 和 0.2 都转化成二进制后再进行运算
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111

// 转成十进制正好是 0.30000000000000004

为什么 x=0.1 能得到 0.1？

恭喜你到了看山不是山的境界。因为 mantissa 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992，对应科学计数尾数是 9.007199254740992，这也是 JS 最多能表示的精度。它的长度是 16，所以可以使用 toPrecision(16) 来做精度运算，超过的精度会自动做凑整处理。于是就有：

0.10000000000000000555.toPrecision(16)
// 返回 0.1000000000000000，去掉末尾的零后正好为 0.1

// 但你看到的 `0.1` 实际上并不是 `0.1`。不信你可用更高的精度试试：
0.1.toPrecision(21) = 0.100000000000000005551

大数危机

可能你已经隐约感觉到了，如果整数大于 9007199254740992 会出现什么情况呢？
由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1，这就是能表示的最大整数。但你并不能这样计算这个数字，因为从 2^1024 开始就变成了 Infinity

> Math.pow(2, 1023)
8.98846567431158e+307

> Math.pow(2, 1024)
Infinity

那么对于 (2^53, 2^63) 之间的数会出现什么情况呢？

• (2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数
• (2^54, 2^55) 之间的数会四个选一个，只能精确表示4个倍数
• ... 依次跳过更多2的倍数

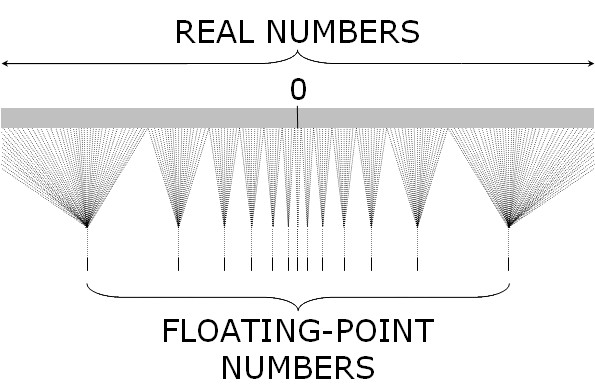
下面这张图能很好的表示 JavaScript 中浮点数和实数（Real Number）之间的对应关系。我们常用的 (-2^53, 2^53) 只是最中间非常小的一部分，越往两边越稀疏越不精确。

在淘宝早期的订单系统中把订单号当作数字处理，后来随意订单号暴增，已经超过了
9007199254740992，最终的解法是把订单号改成字符串处理。

要想解决大数的问题你可以引用第三方库 bignumber.js，原理是把所有数字当作字符串，重新实现了计算逻辑，缺点是性能比原生的差很多。所以原生支持大数就很有必要了，现在 TC39 已经有一个 Stage 3 的提案 proposal bigint，大数问题有望彻底解决。在浏览器正式支持前，可以使用 Babel 7.0 来实现，它的内部是自动转换成 big-integer 来计算，要注意的是这样能保持精度但运算效率会降低。

toPrecision vs toFixed

数据处理时，这两个函数很容易混淆。它们的共同点是把数字转成字符串供展示使用。注意在计算的中间过程不要使用，只用于最终结果。

不同点就需要注意一下：

• toPrecision 是处理精度，精度是从左至右第一个不为0的数开始数起。
• toFixed 是小数点后指定位数取整，从小数点开始数起。

两者都能对多余数字做凑整处理，也有些人用 toFixed 来做四舍五入，但一定要知道它是有 Bug 的。

如：1.005.toFixed(2) 返回的是 1.00 而不是 1.01。

原因： 1.005 实际对应的数字是 1.00499999999999989，在四舍五入时全部被舍去！

解法：使用专业的四舍五入函数 Math.round() 来处理。但 Math.round(1.005 * 100) / 100 还是不行，因为 1.005 * 100 = 100.49999999999999。还需要把乘法和除法精度误差都解决后再使用 Math.round。可以使用后面介绍的 number-precision#round 方法来解决。

解决方案

回到最关心的问题：如何解决浮点误差。首先，理论上用有限的空间来存储无限的小数是不可能保证精确的，但我们可以处理一下得到我们期望的结果。

数据展示类

当你拿到 1.4000000000000001 这样的数据要展示时，建议使用 toPrecision 凑整并 parseFloat 转成数字后再显示，如下：

parseFloat(1.4000000000000001.toPrecision(15)) === 1.4  // True

封装成方法就是：

function strip(num, precision = 15) {
  return +parseFloat(num.toPrecision(precision));
}

为什么选择 15 做为默认精度？这是一个经验的选择，一般选15就能解决掉大部分0001和0009问题，而且大部分情况下也够用了，如果你需要更精确可以调高。

数据运算类

对于运算类操作，如 +-*/，就不能使用 toPrecision 了。正确的做法是把小数转成整数后再运算。以加法为例：

/**
 * 精确加法
 */
function add(num1, num2) {
  const num1Digits = (num1.toString().split('.')[1] || '').length;
  const num2Digits = (num2.toString().split('.')[1] || '').length;
  const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
  return (num1 * baseNum + num2 * baseNum) / baseNum;
}

以上方法能适用于大部分场景。遇到科学计数法如 2.3e+1（当数字精度大于21时，数字会强制转为科学计数法形式显示）时还需要特别处理一下。

能读到这里，说明你非常有耐心，那我就放个福利吧。遇到浮点数误差问题时可以直接使用
https://github.com/dt-fe/number-precision

完美支持浮点数的加减乘除、四舍五入等运算。非常小只有1K，远小于绝大多数同类库（如Math.js、BigDecimal.js），100%测试全覆盖，代码可读性强，不妨在你的应用里用起来！

参考

• Double-precision floating-point format
• What Every Programmer Should Know About Floating-Point Arithmetic
• Why Computers are Bad at Algebra | Infinite Series
• Is Your Model Susceptible to Floating-Point Errors?

当然写这篇文章是为了招聘！！！

阿里巴巴大数据前端部门诚招前端攻城狮。不要犹豫，万一通过了呢。
简历发过来 [email protected]

[YingshanDeng]

@camsong 感谢作者的分享，文章很不错 👍 其中 大数字危机 一节中：

由于 M（应该是笔误 ❓） 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1。这就是能表示的最大整数。

这句有点困惑，指数位最大值为 2047，减去 1023 后应该是 1024 吧，所以最大能表示的数为 2^1024 - 1 ？

JavaScript能表示并进行精确算术运算的整数范围为：正负2的53次方；超过范围的，无法给出精确计算结果，您文章给出的配图： JavaScript 中浮点数和实数（Real Number）之间的对应关系 也解释了这一点。

Math.pow(2, 53) 
-> 9007199254740992
Math.pow(2, 53) + 1
-> 9007199254740992
Math.pow(2, 53) + 2
-> 9007199254740994

这个段代码也验证了：(2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数。而这一点应该也可以作为回答知乎问题的理由之一吧：javascript 里最大的安全的整数为什么是2的53次方减一？

[camsong]

@YingshanDeng typo fixed。能解释，我也正是想说明这个问题。

[Jenny-O]

666，感谢分享干货，已推荐到 SegmentFault 头条 (๑•̀ㅂ•́)و✧
链接如下：https://segmentfault.com/p/1210000011570610

[natee]

赞好文。
补充一个基本知识点，解释了64位中的“符号”、“指数”、“尾数”分别是什么，从而得到双精度浮点数实际值的公式。

双精度浮点数

[camsong]

@natee 本来就加了，只是 Github 不支持 Latex，已换成截图

[shoung6]

感觉只要strip转换一下最终的计算结果，计算就正确了。是不是不需要精确的加减乘除

[camsong]

@shoung6 strip 只能用于最终结果，不要对中间结果进行处理，否则会刚开始差之毫厘，结果谬以千里。而后面的加减乘除都是精确的计算

[shoung6]

嗯嗯，那什么情况是strip实现不了，必须用精确加减乘除的吗？我感觉我能想到的计算需求，只要计算完成之后strip一下就正确了，就不需要加减乘除那几个函数了~

[camsong]

@shoung6 外部传入的“异常”数据需要展现的时候。如后端接口返回 3.4500000001，前端要格式化后展示的情况。浮点数异常对 Java、Python、Ruby 等语言都适用。

[shoung6]

这个是用strip，我是说必须用精确加减乘除的需求

[camsong]

文中 strip 会把精度降到 10^12，但 JS 本身的精度可以到 2^53。当你做多次计算时当初的小误差，结果可能就有大不同。还是看场景吧，如果你数字很小，最后 strip 一下也是可以的

[shoung6]

嗯嗯，谢谢解答~

[mmmmmaster]

想请教个问题：
文中提到，10进制的0.1，转成二进制结果是0.0001100110011001100（无限循环），
既然是无限循环，根据二进制转十进制的公式，
结果应该是：0+0+0+1/16 +1/32+0+0+1/256+1/512+......+.........，
最终结果应该小于0.1才对（因为后面肯定加不完，等于少加了一些），但结果确是0.100000000000000005551115123126，
这个数字明显大于0.1，很不解，是我理解的不对吗，求解啊

[mmmmmaster]

还有个问题：
Math.pow(2,53)+0 >>9007199254740992
Math.pow(2,53)+1 >>9007199254740992
以上可以说明2^53-2^54之间，每两个选一个，但接下来：
Math.pow(2,53)+2 >>9007199254740994（注意这个值）
Math.pow(2,53)+3 >>9007199254740996
Math.pow(2,53)+4 >>9007199254740996，
这就有问题了，+3时应该和+2保持一致啊，但是程序的结果却很意外，并不是每2个选一个，
求解，先感激下！

[YingshanDeng]

@mmmmmaster 我来回答一下这两个问题吧 😋
① 十进制的 0.1 转换成二进制后，结果的确是 0.0001100110011001100（无限循环），这个二进制再进行 64 位浮点数存储得到：0011111110111001100110011001100110011001100110011001100110011010 ，然后再将这个64位二进制转换回十进制的时候，得到的就是：0.100000000000000005551115123126。这个转换可以通过在线网站：http://www.binaryconvert.com/convert_double.html 进行

②首先我们要知道 [-2^53, +2^53] 这个范围是称为 safe integers，超出这个范围的数字，就是 unsafe integers。对于对于 (2^53, 2^63) 之间的数会出现什么情况呢？

(2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数
(2^54, 2^55) 之间的数会四个选一个，只能精确表示4个倍数
... 依次跳过更多2的倍数

所以我们看到 (2^53, 2^54) 范围的数字，都是间隔 2 的。

然后我们还要了解到不是 safe integers 的数字，计算结果不能确保其正确性。所以你提到的那几个计算中有些正确，有些不正确。

第二个问题关键在于不要混淆这两个概念即可。

最后，@camsong 这么理解对吧 😂

[mmmmmaster]

@YingshanDeng
感谢大哥解答！
第一个问题，从在线网站上转完，确实结果是0.100000000000000005551115123126，但是如果从我们人类的角度来计算，这个结果应该是偏小的（毕竟无限循环加不完啊），不知道误差原因所在。。
第二个问题，如果从超出安全范围则计算结果不准确来考虑，程序吐出那样的结果确实是情有可原的，可理解！
最后， @camsong ，这么理解对吧 😂

[YingshanDeng]

@mmmmmaster 根据我的理解，来解释一下你提到的 0.1 “误差偏大”问题 😀
我们知道十进制 0.1 转换成二进制的时候，小数点后是 0011 循环，然后我们再看看 0.1 用64位二进制表示成：0011111110111001100110011001100110011001100110011001100110011010 注意到尾数最后八位：10011010，我们把正常循环写出来是 100110011，对比之下很明显，有一个四舍五入进位，所以这就导致误差偏大

[mmmmmaster]

@YingshanDeng ，还真是，之前没注意有进位，多谢！

[Rainsho]

终于把我关于 toFixed 的疑惑解释清楚了，可惜公司看不到图片，回家在看一遍储存的问题。感觉 number-precision 就是我第一版修正计算精度的思路，不过我们测试还是不满意效果，最终引入了一个大小和精度介于 number-precision 和 bignumber.js 之间的库 big.js

[WangYang-Rex]

赞

[guitong]

因为 mantissa 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992

大神，省略的一位是什么意思呢

[camsong]

@guitong

下面再以 0.1 例解释浮点误差的原因， 0.1 转成二进制表示为 0.0001100110011001100(1100循环)，1.100110011001100x2^-4，所以 E=-4+1023=1019；M 舍去首位的1，得到 100110011...。

非0数用十进制的科学计数法表示时首位为 1~9，用二进制表示时首位只能是 1，所以就约定把首位这个 1 省去。

[robberfree]

科学计数法的话，10进制的M应该是1=<M<10吧。

[camsong]

对整数为言，1=<M<10 与文中的 0<M<10 对等。

[WuHuaJi0]

有一个疑问，为何C语言中，同样64位双精度的0.1 + 0.2 能计算到结果呢？不知博主是否知道
举例：

double a = 0.1;
double b = 0.2;
printf("%lf",a+b); // 0.3

[robberfree]

@WuHuaJi0 你printf的时候指定了输出格式，所以会截取。

[vuejshub]

文中出现错误

[robberfree]

@FullStack1994 toPrecision 的返回值是字符串类型。

[yeecai]

蹲一个解决办法吧

[allenpzx]

@mmmmmaster 我来回答一下这两个问题吧 😋
① 十进制的 0.1 转换成二进制后，结果的确是 0.0001100110011001100（无限循环），这个二进制再进行 64 位浮点数存储得到：0011111110111001100110011001100110011001100110011001100110011010 ，然后再将这个64位二进制转换回十进制的时候，得到的就是：0.100000000000000005551115123126。这个转换可以通过在线网站：http://www.binaryconvert.com/convert_double.html 进行

②首先我们要知道 [-2^53, +2^53] 这个范围是称为 safe integers，超出这个范围的数字，就是 unsafe integers。对于对于 (2^53, 2^63) 之间的数会出现什么情况呢？

(2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数
(2^54, 2^55) 之间的数会四个选一个，只能精确表示4个倍数
... 依次跳过更多2的倍数

所以我们看到 (2^53, 2^54) 范围的数字，都是间隔 2 的。

然后我们还要了解到不是 safe integers 的数字，计算结果不能确保其正确性。所以你提到的那几个计算中有些正确，有些不正确。

第二个问题关键在于不要混淆这两个概念即可。

最后，@camsong 这么理解对吧 😂

2 ** 53应该是开区间吧，不包括 2 ** 53，应该是(-2 ** 53, 2 ** 53), 尾数表精度，这也是JS里面最大安全整数

[allenpzx]

👇最大安全整数，IEEE 754标准一共有53位的尾数（包含省略的1位），类似于科学计数法，尾数表示的是精度，一个数对应一个IEEE 754的双精度浮点数，所以是安全的，当多个数对应一个浮点数的时候就是不安全的
Math.pow(2, 53) - 1 === Number.MAX_SAFE_INTEGER

👇最大数，根据IEEE 754标准的定义来的。为什么指数减去52，因为尾数表示的是1.1111（52位），尾数左移指数减去对应的位数，所以这个就是最大值
1 * Math.pow(2, 1023 - 52) * (Math.pow(2, 53) - 1) === Number.MAX_VALUE

[daiwa233]

由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1

为什么 E 最大值是 1023？E 的取值是 [0,2047]，然后减去中间数 1023， 那最大值不是 1024 吗

[Gavinchen92]

由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1

为什么 E 最大值是 1023？E 的取值是 [0,2047]，然后减去中间数 1023， 那最大值不是 1024 吗

The exponent field is an 11-bit unsigned integer from 0 to 2047, in biased form: an exponent value of 1023 represents the actual zero. Exponents range from −1022 to +1023 because exponents of −1023 (all 0s) and +1024 (all 1s) are reserved for special numbers.

2047被作为特殊类型处理， 即NaN, Infinity, -Infinity

[2678041235]

由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1
最大的整数为什么是2^1024 - 1？最大数不是才到2^1023 * 2^-52*(2^53 - 1),也就是2^1024-2^971嘛？2^1024 - 1怎么比能表示的最大值还大呀, 这里不是很明白，希望能帮忙解答下。

[2678041235]

最大可以表示的整数是 2^1024 - 1

由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1

为什么 E 最大值是 1023？E 的取值是 [0,2047]，然后减去中间数 1023， 那最大值不是 1024 吗

The exponent field is an 11-bit unsigned integer from 0 to 2047, in biased form: an exponent value of 1023 represents the actual zero. Exponents range from −1022 to +1023 because exponents of −1023 (all 0s) and +1024 (all 1s) are reserved for special numbers.

2047被作为特殊类型处理， 即NaN, Infinity, -Infinity

这个2^1024 - 1是最大整数是怎么计算来的，理论上2^970 * (2^54 - 1) 就已经是Infinity了

[erdong-fe]

👍

[erdong-fe]

看完这篇blog后写了一篇文章，感兴趣的可以看看 前端应该知道的JavaScript浮点数和大数的原理

[HolyZheng]

有一个疑惑，尾数M会先省略掉前面的1才存储到52位里面。那么1和0在存储的时候是怎么区分开来的呢？
1 存储时 S = 0, E = 11个0, M = 52个0 （科学计数法前面的1省去）
0 存储时 S = 0，E = 11个0，M = 52个0吗？（0的科学计数法0.0 * 2^0 ? ）
这么按存储来开，没有办法区分0和1呀

[2678041235]

    您好，您的邮件我已收到，会尽快给您答复！

[cyanxxx]

为什么会有精度丢失? 什么时候发生精度丢失?

本次讨论主要解决两个问题:

1. 使用 JS 编程时为什么会出现精度丢失?
2. 使用 JS 编程时什么时候发生精度丢失? 即 Number.MAX_SAFE_INTEGER的值是多少?

1. 使用 JS 编程时为什么会出现精度丢失?

建议先看下本 issue 里作者对于 JS 里怎么存储数字的介绍, 这里简述一下其原理, 只是为了便于解释精度丢失的议题:

JS 里用 64 bits 的空间存储数字, 使用 IEEE-754格式存储和解析数字, 用的是类似科学技术法的方式表示的数字. 比如: 123456 = 1.23456 * 10^5, 这里的 1.23456 就是有效数字, 10^5 的 5是指数. 可以看出来: 如果我们实现定义好使用十进制的科学技术法来存储数字, 那么我们只需要保存 有效数字 和 指数 这两个数据就能表示一个数字了.

JS 内存储数据与上面类似, 只不过存储用的是二进制, 不是十进制, 即有效数字都是 0 或者 1

为什么会有精度丢失的问题呢?

我们简单地还原数据精度丢失的整个过程, 大家就明白了. 为了方便理解, 我们作几个假设:

1. 假设计算机用十进制存储数据, 然后每个 bit 能存 0~9 .
2. 假设一种新的数据存储格式: 只使用 5 个 bits 存放有效数字, 指数则不限多少个 bits.

那么按照我们定义的格式, 123456 存储到计算机内是多少呢?

因为我们只有 5 个 bits 存放有效数字, 123456 的有效数字有 6 位, 所以肯定要舍去多余的 1 位, 为了尽可能保证数据精度, 我们只会丢失最后 1 位, 因为它最小.

所以按我们定义的格式和给定的空间, 123456 存储到计算机内就变成了: 1.2345 * 10^5. 之后我们再 取值时, 它就变成了 123450 了. 丢失了最后 1 位的数据 6.

看到这里应该就知道为什么会丢失精度了吧, 就是因为只要规定了用多少 bits 来存储有效数字, 那计算机内能存储的有效数字就是有限的, 必然会有精度丢失的情况发生.

2. 使用 JS 编程时什么时候发生精度丢失? 即 Number.MAX_SAFE_INTEGER 的值是多少?

回到 JS 的实现中, 底层使用二进制存储数据, 数据格式为: IEEE-754, 用 64 bits 的空间存储数据, 由于某些原因, 使用 52bits 的空间存储有效数字, 但是实际存储了 52 + 1 = 53bits 的有效数字信息(因为第 1 个有效数字始终是 1, 不需要存储), 11 bits 的指数位信息.

那么它们各自的取值范围是多少呢?

有效数字: [0, 2^53 - 1] 指数位: [-1022, 1023] , 指数位还要考虑负指数的情况, 所以使用的是补码形式存储的数据, 还有一些其他的原因. 导致最终的结果不是[0, 2047]

按照上面我们以自定义数据格式举的例子, 应该明白为什么会有精度丢失了, 那在 JS 里数字大于多少时会丢失呢, 也就是 Number.MAX_SAFE_INTEGER 是多少呢?

这个主要跟有效数字表示的范围有关系, 与指数位关系不大(也有关系,后面会提到). 因为指数负责控制小数点的移动. 还是举我们那个例子, 1.23456 * 10^5, 有效数字有 5bits, 只要指数能表示的数字大于5, 那么就肯定能准确表示 [0, 123456]的所有整数. 对应到 IEEE-754 使用64 bits 的方案中, 只要指数能够大于 52 即可.

所以Number.MAX_SAFE_INTEGER是多少, 就看 IEEE-754 使用 64 bits 的方案里, 有效数字最大是多少. 如果存储有效数字的 53bits 全为 1, 那应该是能准确表示的最大数字了吧? 此时表示的数字是: 2^53 -1. 如果在控制台打印一下 Number.MAX_SAFE_INTEGER, 就会发现这个数字就是 2^53 -1.

console.log(Number.MAX_SAFE_INTEGER === 2**53 - 1) // true

好像我们推测对了, 那到底对不对呢?

查阅一下规范中对Number.MAX_SAFE_INTEGER的定义:

The value of Number.MAX_SAFE_INTEGER is the largest integer n such that n and n + 1 are both exactly representable as a Number value.

翻译一下就是: 使得 n 和 n+1 都能被精确表示为 Number 类型的最大的那个数字. 有点绕口, 其实就是不断得增加 n 的值, 一直到 n+1能被精确表示(不会丢失精度), 但 n+2 开始丢失精度, 取这时的 n 为Number.MAX_SAFE_INTEGER.

再回看我们刚刚的推导, 将以下几个数字转为二进制

• 2^53 -1 : 11......111, 一共是 53bits: 全是 1
• 2^53 : 100......000, 一共是 54bits: 1 个 1, 53 个 0
• 2^53 + 1: 100......001, 一共是 54bits: 1 个 1, 52 个 0, 最后再接 1 个 1

我们前面提到JS 底层实现只能存储下 53bits 的有效数字, 所以:

• 对于 2^53 -1: 我们能完整存下它的 53 个 1 , 所以对于 [0, 2^53 - 1]的数字都可以完整存下有效数字, 不会出现精度丢失.
• 对于 2^53: 我们只能存下它的前 53 位, 最后 1 位的那个 0 被舍去了, 但是因为最后 1 位是 0, 所以舍去并不会导致其精度丢失
• 对于 2^53 + 1: 我们只能存下它的前 53 位, 最后 1 位的那个 1 被舍去了, 导致精度丢失.

结合上面规范里的定义, 我们终于找到了符合 Number.MAX_SAFE_INTEGER 定义的那个数字n: 2^ 53 - 1, 而不是 2^53.

参考资料

• JavaScript 浮点数陷阱及解法
• WikiPedia-Floating-point arithmetic
• WikiPedia-IEEE_754
• ECMAScript® 2021 Language Specification#sec-number.max_safe_integer

这样为什么一开始设计的时候不把尾数位划大一点，指数位划小几位呢？

[2678041235]

    您好，您的邮件我已收到，会尽快给您答复！

[zp29]

蹲一个解决办法吧
答案就在上面！

console.log(8.87 * 100) // 886.9999999999999
console.log(parseFloat((8.87 * 100).toPrecision(12))) // 887

[2678041235]

    您好，您的邮件我已收到，会尽快给您答复！