Esta clase esta un poco orientada a ver los distintos modelos de calculo lambda, al menos vamos a tratar de ver los modelos mas basicos de lenguajes que vamos a poder diseñar sin tener que implementar un compliador completo, por lo que esta clase se va a centrar en explicar sobre calculo lambda, que es en si un sistema formal en el que se pueden aplicar funciones y definir variables, en si es un pequeño lenguaje de programacion en el que vamos a poder definir funciones, aplicarlas con valores. Se usa especialmente sobre teoria de tipos ya que es el caso de un lenguaje de programacion abstracto y simple de describir, si bien fue pensado originalmente como un sistema sin tipos.
Vamos a ver que para llegar un poco a la parte final de mostrar el codigo, tal vez es necesario aclarar algunos conceptos previos de compiladores, y de algunas herramientas que estaremos usando para armar nuestro calculo lambda.
En la compilación o interpretación de un lenguaje existen distintas etapas, desde que nosotros tenemos nuestro input hasta que generamos una salida que nos sirve la para ejecución ya sea instrucciones de máquina u otro tipo de instrucciones que nos permitan de alguna manera interpretar esas instrucciones y poder tener un resultado de la entrada computacionalmente.
- Lector: que genera una estructura a partir de un input que es texto en genera, aunque puede ser a veces binario. Esta estructura la llamaremos IR.
- Generador: recorre la estructura y genera una salida a partir de este que puede serla salida misma de un compilador.
- Traductor: Un traductor leer una entrada de texto o binario y la traduce a otra salida que puede ser una traducción de un lenguaje a otro. Es un lector combinado con un generador. Ej. un profiler, refactor engine, etc.
- Intérprete: Un interprete lee, decodifica y ejecuta instrucciones desde simples cálculos hasta operaciones mas complejas, podemos ver esto en entornos como el de Ruby y Python cuyo interprete ejecuta un output final que es bytecode.
En este ejemplo no vamos a enfocar un poco en el Lector(Lexer y Parser) y estaremos llegando a ese nivel final que es el de tener una estructura intermedia que va a ser ejecutado para generar el resultado del calculo lambda.
Existen muchos tipos de representaciones intermedias, la que nos interesa en particular por el momento es generar una construcción en forma de árbol llamada AST (Abstract syntax Tree). El AST sería un IR? No exactamente, si bien muchas IR son similares a los AST, los IR se refiere más al concepto de tener una representación de datos que está más asociada a una máquina abstracta en la que se realizará el análisis semántico, junto con las optimizaciones antes de pasar a la etapa de code generation. Nos interesa tener una construcción abstracta ya que nos permitirá trabajar con ella, y contendrá más información sobre el input que recibimos y no solamente texto. De esta manera será más fácil de saber el orden de ejecución y la información de cada uno de los nodos. Porqué vemos un AST como primer tipo de construcción abstracta? Porque es lo más simple para trabajar, si bien hay otro tipo de construcciones como ASG que nos permitirán trabajar más cómodo con lenguajes más complejos.
Por ej. si tenemos una expresión como this.x = y el AST que se forma una vez parseada la misma es:

Aquí se puede ver que cada uno de los nodos del árbol representa un miembro de la expresión ya sea un identificador como x o y ó operadores como . o =. Como se remarcó antes estos nodos no solo tendrá definido el texto de entrada sino a que tipo pertenecen y el orden de evaluar la expresión dependerá de cómo es la estructura del AST, en este caso el orden de evaluación es de izquierda a derecha y de abajo hacia arriba. Existen distintos algoritmos para armar el AST y recorrer estos, luego pasaremos más links ya que nuestro objetivo al menos es la de aprender el paso para armar estas expresiones.
Volviendo al proceso que veremos hoy, el pipeline o pasos que veremos de la compilación son los siguientes:
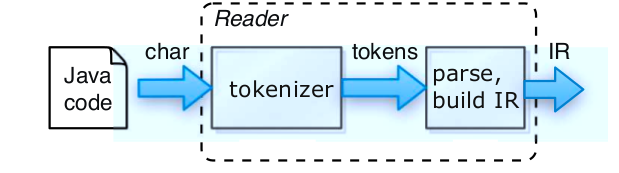
Solo veremos el lector, y este lector empieza por algo llamado tokenizer, que es esta fase?
El tokenizer o analizador léxico es un módulo de nuestro compilador/intérprete/etc que lee nuestra entrada y separa esta en unidades que nuestro parser va a poder entender, dichas unidades son llamadas lexemas. Luego lo que hará el parser es validar la sintaxis de estos lexemas y decirnos si es correcta o no. Entonces si tenemos una entrada que es como
public static class Pepita { …..
generará lexemas de esta manera
public static class Pepita { …..
Las implementaciones que existen cuando se tokenizan se pasan al parser y este irá generando nuestra IR. Siempre lo recomendable es armar una IR si hacemos múltiples pasadas por el input, ya que la retokenización y reparseo del input para cada uno de los pasos es ineficiente y se complica el pasaje de información de cada uno de los pasajes. Múltiples pasadas nos permiten determinar errores de sintaxis en el analizador sintáctico que usará al IR para esto. Por ahora esto no es muy importante sino que hay que solamente tener en cuenta que el analizador léxico.
Otra cosa a tener en cuenta es que el analizador léxico tiene acceso a la tabla de símbolos que utiliza tanto este como el parser para generar la IR. Porque tiene acceso a esta tabla? Ahora explicaremos esto…
Antes de pasar al parser o analizador sintáctico pongamos un ejemplo de un pedazo de código en C como
fi ( a == f(x)) …
Vemos que cuando el analizador léxico lea la entrada no detectará a la palabra fi como una entrada inválida, y creará el lexema fi como un identificador…. pero si vemos nosotros esta expresión debería existir un if en vez de un fi…. entonces??? El analizador léxico no sabe determinar si sintácticamente es válida o no la expresión, sino que deberá pasarlo a otra etapa del compilador en este caso el parser que mediante la tabla de símbolos y reglas sintácticas determina que fi es inválido. Lo que sí puede hacer el analizador sintáctico es que si hubiese caracteres inválidos, no ascii o extraños a la entrada, o que no pueda pasar un lexema al parser porque es inválido en su construcción, entre en un modo llamado “modo de pánico”, en el que utiliza una estrategia en la que se eliminan caracteres sucesivos de la entrada hasta que el analizador pueda encontrar un token bien formado y generar una lexema correctamente. Hay otras estrategias de recuperación tales como:
- Eliminar un carácter del resto de la entrada
- Insertar un carácter faltante en el resto de la entrada
- Sustituir un caracter por otro
- Transponer dos caracteres adyacentes
Estas transformaciones se pueden probar antes de ignorar estas entradas inválidas.
Ahora el parser y el lexer usan una tabla de símbolos y el primero usa también reglas sintácticas para validar la entrada y generar una IR. Como se definen estas construcciones??
Por medio de una gramática. Y que es? es un conjunto de reglas sintácticas que definen a como es un programa válido para nuestro lenguaje.
Existen distintos tipos de gramáticas, las que nos importan en nuestro ámbito son las gramáticas formales, y veremos que hay varios tipos de clasificación. Esta clasificación la hizo Noam Chomsky quien formalizó la idea de las gramáticas generativas en 1956, clasificó este tipo de gramáticas en varios tipos de complejidad creciente que forman la llamada jerarquía de Chomsky. La diferencia es que cada uno tiene reglas más particulares y restringidas, por lo que cada una genera lenguajes formales menos generales. Los más importantes y que veremos son las gramáticas libres de contexto (Tipo 2) y las regulares (Tipo 3). Estas son mucho menos generales que las gramáticas no restringidas de Tipo 0, que son solo reconocidas y que pueden procesarse mediante una máquina de turing.
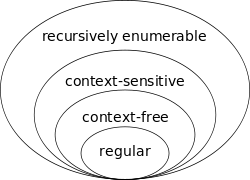
Las gramáticas que veremos en este encuentro se basan en las de tipo 2 y 3, las libres de contexto y regulares. Las gramáticas regulares nos permiten describir lenguajes regulares y las mismas podemos verlas expresadas en expresiones regulares para búsqueda de patrones en un texto a buscar este patrón, lo que nos permite hacer este tipo de expresiones la búsqueda tanto de construcciones regulares finitas como infinitas
Podemos definir a cualquier gramática formalmente como una 4-tupla (Vn, Vt, P, S), donde:
- Vn es el vocabulario de noterminales; es un conjunto finito de "productores"
- Vt es el vocabulario de terminaes, caracteres del alfabeto sobre el cual se construyen las palabras del lenguaje formal que es generado por la gramática descripta; también es un conjunto finito.
- P es el conjunto finito de producciones
- S pertenece a Vn es un noterminal especial llamado axioma. Es el noterminal a partir del cual siempre deben comenzar a aplicarse las producciones que genera las palabras de un deteminado Lenguaje Formal
Cuando decimos que una gramática formal genera un lenguaje formal, significa que puede generar todas las palabras del Lenguaje Formal, pero no genera a aquellos que están fuera de las restricciones de este. De esta manera una gramática libre del contexto puede usarse para describir un lenguaje regular aunque una gramática regular no puede usarse para describir un lenguaje libre de contexto ya que la gramática regular posee mayores restricciones.
Una gramática regular derecha es aquella cuyas reglas de producción P son de la siguiente forma:
A → a, donde A es un símbolo no-terminal en N y a uno terminal en Σ A → aB, donde A y B pertenecen a N y a pertenece a Σ A → ε, donde A pertenece a N.
Análogamente, en una gramática regular izquierda, las reglas son de la siguiente forma:
A → a, donde A es un símbolo no-terminal en N y a uno terminal en Σ A → Ba, donde A y B pertenecen a N y a pertenece a Σ A → ε, donde A pertenece a N.
Una definición equivalente evita la regla 1 (A → a) ya que es sustituible por:
A → aL
L → ε
en el caso de las gramáticas regulares derechas y por:
A → La
L → ε
en el caso de las izquierdas.
Algunos autores alternativamente no permiten el uso de la regla 3 suponiendo que la cadena vacía no pertenece al lenguaje. Un ejemplo de una gramática regular G con N = {S, A}, Σ = {a, b, c}, P se define mediante las siguientes reglas:
S → aS
S → bA
A → ε
A → cA
donde S es el símbolo inicial. Esta gramática describe el mismo lenguaje expresado mediante la expresión regular abc. Dada una gramática regular izquierda es posible convertirla, mediante un algoritmo en una derecha y viceversa. Estas gramáticas estan ya implementadas en herramientas y librerías que proveen de algo llamado expresiones regulares, y lo que permite es detectar tokens de un lenguaje regular para que podamos luego tratarlo por nuestra cuenta.
Por ejemplo de esta manera una gramática como:
S → aS es regular mientras una gramática como S → aSb no lo es.
Bien y las gramáticas libres de contexto?
##Gramáticas libres de contexto
Las gramáticas libres de contexto son aquellas que tienen una construcción del tipo V → w en donde V es un no terminal y w es un conjunto de terminales y/o no terminales. El término libre de contexto se refiere al hecho de que el no terminal V puede siempre ser sustituido por w sin tener en cuenta el contexto en el que ocurra. Las gramáticas libres de contexto generan lenguajes libres de contexto y la manera de comprenderlos es mediante parsers… veremos teóricamente antes de la práctica por parsers LL. Pero antes la definición formal para aquel que le interese
Una gramática libre de contexto se la define como: donde
es un conjunto finito de terminales
es un conjunto finito de no terminales
es un conjunto finito de producciones
el denominado Símbolo Inicial
- los elementos de
son de la forma
Mediante estas gramáticas los analizadores sintácticos arman derivaciones que generan justamente estructuras intermedias siendo la más inmediata y simple, los AST.
Imaginemos el caso en el que tenemos una gramática como la siguiente
W → a | aS
S → ε | bS | cS
Esta describe un lenguaje del tipo a(bc)* y veamos como podría ser la transición de una entrada como abbcb:
W → aS → abS → abbS → abbcS → abbcbS → abbcb
cada uno de estos pasaje se lo denomina derivaciones y son los pasos que se realizan de acuerdo a las reglas de la gramática que generan nuestros tokens de acuerdo a la entrada.
En este caso que mostramos muestra una derivación a izquierda aunque podríamos tener también derivación a derecha. Repasemos estos conceptos
- Derivación a izquierda: en cada paso de la derivación se reemplaza el noterminal que se encuentra primero, de izquierda a derecha, en la cadena de derivación.
- Derivación a derecha: en cada paso de la derivación se reemplaza el noterminal que se encuentra primero, de derecha a izquierda, en la cadena de derivación.
Veamos un caso clásico que sucede a veces al crear una gramática para un lenguaje:
expr → expr + term | term
Veamos que si empezamos a realizar una derivación sobre esta regla gramatical:
expr → expr + term → expr + term + term → expr + term + term, la gramática en ese caso se dice que tiene una recursividad hacia izquierda si se elije su primera regla y en el caso que tengamos una implementación de un top-down parser como se explico en el encuentro anterior, estaremos ante un evento que loopeará indefinidamente. para ello se puede reformular la gramática para que pase de ser recursiva a izquierda a derecha y de esta manera que sea posible de que funcione computacionalmente con un top-down parser.
entonces teniendo una gramática genérica del tipo
X → Xα | β
la traducción mecánica a recurividad derecha es:
X → βX'
X'→ αX' | ε
La transformación agrega un nuevo no terminal X' en donde delega la recursividad, y para que no cicle indefinido se introduce un caso de corte con la cadena vacía.
Ahora en el caso que se tenga un ejemplo como X → Xα en donde no esta presente el otro miembro beta, imaginemos que β = ε
X → Xα |ε
pasando a recursividad por derecha
X → εX'
X'→ αX' | ε
entonces :
X → X'
X'→ αX' | ε
entonces queda reducido a:
X→ αX | ε
De esta manera se sigue tienendo una gramática recursiva por derecha y es el otro caso de este tipo.
Ahora veamos un caso en el que por ej:
S → Xa
X →S | aS
derivando de nuevo
S → Xa → aSa → aXaa → aSaa →aXaaa....
Se ve de nuevo que hay una recursividad por ixquierda, esto se traduce como una recursividad por izquierda indirecta, para resolver la misma basta con aplanar la gramática
S → (S | aS) a
S →Sa | aSa
se puede ver de nuevo como existe una recursividad por izquierda en el primer caso, pasamos a recursividad por derecha y se solucionará el problema:
S → aSaS'
S' →aS' | ε
###Factorización por izquierda
Hay veces que podemos llegar a tener una gramática del siguiente tipo:
S → iEtS | iEtSeS | a
en donde el primer y segundo camino que puede tomar la derivación empiezan de la misma manera, podríamos simplificar la gramática de la siguiente manera:
S → iEtsB | a
B → ε | eS
De esta manera queda más facil la gramática y puede reemplazarse ese nuevo terminal en otros lugares que se repita la construcción. A esto se lo conoce como factorización por izquierda.
##Gramáticas ambiguas
Si bien no se menciono en clase, existen gramáticas que son ambiguas y cual sería este caso? En este caso si tenemos una gramática que nos permite modelar una estructura clásica como if/else de este estilo:
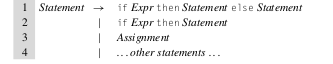
Vemos que nuestro if puede ser un if Expr then Stmt siempre y el bloque else sería opcional. Ahora imaginemos que tenemos un caso en el que tenemos un if anidado en el bloque then de otro if:
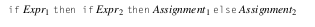
En este caso nuestro parser no sabrá a que contexto pertenece nuestro bloque else cuando lo parseemos con un top-down parser, y se podrían generar dos resultados distintos de AST, uno en el que el bloque else pertenece al segundo if anidado, que sería nuestro escenario deseado:
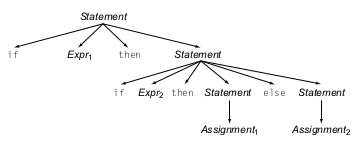
Y otro resultado en el que el bloque else pertenece al primer if
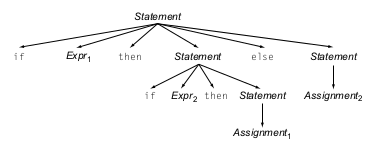
En este caso se dice que la gramática es ambigua ya que una vez armado uno de los dos AST no sabremos si el resultado que generamos era el deseado o no.
Para eliminar la ambigüedad en este ejemplo, basta con reescribir nuestra gramática de una manera que podamos distinguir cuando tenemos una gramática del tipo if/then o if/then/else. Entonces nuestra gramática podría quedar como:

Para que me sirve un lenguaje regular? el ejemplo más casual es para buscar patrones en un texto de entrada, mediante lo que conocemos como expresiones regulares y que permiten que expresar lenguajes regulares, sean finitos o infinitos.
Vimos algunos ejercicios con RegEx y fuimos probando en la siguiente página:
De aqui se puede buscar referencias sobre como utilizar las regex y con datos de muestra de entrada.
Otro lugar con referencia para regex se encuentra aqui: Regex
Luego de esto explicamos que existen casos en el que no podemos parsear un programa o entrada por medio de una expresión regular, por ej. un programa en Java. Para ello necesitamos una implementación que permita describir gramáticas libres de contexto, que tienen menos restricciones que las regulares, estas implementaciones son llamada generalmente parsers.
Es un analizador sintáctico que permite reconocer un lenguaje libre de contexto, descripta mediante una gramática de este tipo y genera un árbol de derivación o AST. Veremos como primer parser los parsers LL que son el ejemplo de parser más básicos y luego veremos ejemplos con parser combinators en Scala. Un tema a destacar es que los parsers realizan un análisis sintáxtico sobre nuestros tokens generados en el Lexer o tokenizador, y que ante una sintaxis incorrecta el parser puede generar un error y para el proceso de compilación hasta que se arregle la entrada correctamente y se vuelva a ejecutar el proceso nuevamente por parte del usuario.
Bien hay muchos tipos de parsers, por un tema de tiempo dejaremos el resto menos uno de lado...
Ahora ya sabemos sobre parsers, regex y gramáticas, lo que nos interesa es como escribir parsers en scala, por suerte en scala tenemos construcciones mucho más avanzadas que un parser de LL(1) que nos permitirá escribir parsers definiendo nuestras reglas gramaticales y lo que generará estas reglas. La construcción que utilizaremos en scala es algo llamado parser generators.
Que es un generator????, es una función de orden superior que combina dos funciones en una nueva función, entonces un parser generator es una función de orden superior que toma dos parsers y genera otro nuevo combinandolos.
De esta manera podremos combinar técnicas de distintos parsers para armar parsers mucho más completos y potentes, y tengamos que escribir menos código, y en el que en cada regla definimos que tipo de parser genera y cómo sería la entrada
Hay operaciones que podremos hacer con nuestros combinators cuando definamos las reglas de nuestro parser
- | es el combinator de alteración. es exitoso si la parte de la izquierda o derecha es exitosa
- ~ es el combinador secuencial. Que es exitoso si el operando de la izquierda parsea bien, y el de la derecha parsea bien para el resto de la entrada.
- ~> es el combinador que es exitoso si el operando de la izquierda parsea exitosamente seguido del de la derecha pero no incluye el contenido de la izquierda en el resultado.
- <~ es la reversa del anterior
- ^^ es el combinator de transformación. Si el operador izquierdo parsea bien, transforma el resultado usando la función de la derecha
- rep quiere decir que espera N- repeticiones del parser X donde X es el parser pasado como un argumento a rep.
Es un lenguaje pequeño en el que se pueden representar todas las funciones computables, entonces es fácil extender y probar propiedades. En particular, tiene la siguiente sintaxis:
- <variable>
- <exp-λ> <exp-λ>: representa el resultado de aplicar una expresión sobre otra (reduciendo a izquierda?)
- λ<variable>.<exp-λ>: representa el valor de evaluar la expresión, donde la variable se ligue con los argumentos (Esto quizás esta jodido de contar…) (más abajo, en un ejemplo quizás se entiende mejor)
Y esta semántica (o reducciones):
- α-reducción: renombramiento de variables
- β-reducción: vinculaciones de variables (“bindings”)
- η-reducción: dos funciones son iguales si al aplicarles los mismos argumentos dan los mismos resultados.
- β-reducción es la más importante, ya que define la aplicación de expresiones a expresiones.
Vamos a ver un poco mas en detalle lo que acabamos de resumir de a pasos
La sintaxis de l calculo lambda es la siguiente
- t ::= terms
- x variable
- λx.t abstraccion
- t.t applicacion
Finalmente pasamos a ver el modelo del calculo lambda sin tipos que en si solo vamos a poder definir una de los tres terminos para cualquier programa valido. Algo bastante interesante es que la transformación a la sintaxis abstracta se hace en dos pasos distintos, por un lado el lexer va a definir nuestros tokens que van a formar parte de los miembros del árbol abstracto que hace luego el parser en la ultima parte.
Por ejemplo empecemos con algo simple si tenemos algo como un 1+2*3 y tratamos de pasar esto a un árbol sintáctico, podría queda en algo como
+
/ \
1 *
/
2 3
*
/ \
- 3
/
1 2
EL foco es que podemos tener mas de una manera de interpretar la expresión por medio de un árbol sintáctico, ahora, la idea es que nosotros tengamos una manera de que querramos interpretar a nuestros términos de calculo lambda, por lo que algo como s t u debería generar el mismo árbol que (s t) u, o sea que la asociación seria por izquierda, y esta expresión generaría:
TODO: Armar el arbol
Despues, los cuerpos de las abstracciones se usan para extender lo mas que se puedan a la derecha, entonces algo como λx. λy. xix es el mismo árbol que λx.(λy.(xy) x))
Un punto importante para remarcar es sobre los contextos en el que están definidos las variables, una ocurrencia de una variable x se dice que esta bound ( o ligado) cuando esta enmarcada en un cuerpo t de una abstracción λx.t, mas precisamente se quiere decir que esta ligado a su abstracción, equivalentemente se puede decir que λx es un binder a cuyo scope es t. Ahora una variable x se la denomina libre cuando aparece en una posición donde no esta enmarcado por ninguna abstracción en x, por ejemplo, las ocurrencias de x en xy y λy. xy son libres, mientras que en las de λx. x y λz. λy. λx. x (y z) son ligadas, en (λ.x x ) x, la primera ocurrencia de x esta ligada mientras que la segunda es libre.
Definiciones sobre variables ligadas y libres
Un termino sin variables libres se la denomina cerrada Termino cerrados se los denominan también combinados El combinador mas simple es la function identidad: id = λx. x
En el estado mas simple el calculo lambda no posee constantes u operadores primitivos, o números, operaciones aritmeticas, condicionales, loops, secuenciamiento, etc. El simple hecho del termino computar es la aplicación de funciones a argumentos, en la que ellos mismos son funciones. Cada paso en la computación consiste en sustituir el componente del lado derecho por la variable ligada del cuerpo de la abstracción, por ej.
Si tenemos algo como:
(λx. t1) t2 -> [x => t2] t1,
Donde [x => t2] t1 significa que el termino obtenido de reemplazar todas las libres occurrencias de x en t1 por t2. Por ej algo mas simple es
el termino (λx. x) y . Se evalúa en y. El termino (λx. x (λx. x)) (u r) se evalúa en (u r) (λx. x)
A estas “reducciones” se las llaman expresiones reducibles o “redex”, esta regla es la que formalmente se conoce como reducción-beta
Hay distintas evaluaciones de reducción beta que depende de como se evaluaran las variables simples sobre las funciones.
- Reducciones beta completas
Cualquier redex puede ser reducido en cualquier momento. Esto significa esencialmente la falta de una estrategia de reducción particular, con respecto a la reducibilidad, "todas las apuestas están canceladas".
Por ejemplo un caso como id (id (λz. Id z)) posee tres redex
id (id (λz. Id z))
id (λz. Id z)
Id z
ø
Entonces podemos hacer las reducciones desde adentro hacia afuera
id (id (λz. Id z))
id (id (λz. z))
id (λz. z)
λz. z
ø
- Orden normal
El redex más a la izquierda y más externo siempre se reduce primero. Es decir, siempre que sea posible, los argumentos se sustituyen en el cuerpo de una abstracción antes de que se reduzcan los argumentos.
id (id (λz. Id z))
id (λz. Id z)
λz. Id z
λz. z
ø
Bajo esta estrategia y las siguientes, la relación de evaluaciones es realmente una función parcial, en la que cada termino t evalua en un paso a lo sumo un termino t’
- Llamar por nombre Como orden normal, pero no se realizan reducciones dentro de abstracciones. Por ejemplo, λx. (Λx.x) x está en forma normal de acuerdo con esta estrategia, aunque contiene la redex (λx.x) x.
Yendo a nuestro ejemplo de antes, quedaría
id (id (λz. Id z))
(id (λz. Id z))
λz. Id z
ø
Hay un caso particular, o en realidad una variación, llamado:
-
Llamar por necesidad (Call by need) Como orden normal, pero las aplicaciones de función que duplicarían los términos, en cambio nombrarían el argumento, que luego se reducirá solo "cuando sea necesario". Llamado en contextos prácticos "evaluación perezosa". En las implementaciones, este "nombre" toma la forma de un puntero, con el redex representado por un procesador. Esto es lo que utiliza en gral lenguajes como Haskell y Algol-60.
-
Llamar por valor Solo se reducen los redexes más externos: un redex se reduce solo cuando su lado derecho se ha reducido a un valor (abstracción variable o lambda). Es la estrategia que usa la mayoría de los lenguajes de uso general.
id (id (λz. Id z))
(id (λz. Id z))
λz. Id z
ø
La mayoría de los lenguajes de programación (incluidos Lisp, ML y lenguajes imperativos como C y Java) se describen como "estrictos", lo que significa que las funciones aplicadas a los argumentos que no son normalizadores no son normalizadoras. Esto se hace esencialmente usando orden aplicativo, reducción de llamada por valor (ver más abajo), pero generalmente se llama "evaluación impaciente".
Si bien no hay suporte de multiples argumentos para el calculo lambda, es algo que se puede lograr sin muchos problemas tratando de utilizar funciones de orden superior que yieldean funciones como resultados, para que quede mas claro, dado un s que es un termino en el que involucra a dos variables libres x, y; y queremos escribir una función f que para cada par (v, w) de argumentos, bielden el resultado de substituir v for x y w por y en s. Por lo que en vez de escribir algo como f = λ(x, y). s como lo haríamos en un lenguaje de programacion mas serio (?), lo escribiremos f = λx.λy. s. Por lo que estas variables se reducirán a la siguiente manera ((λy. [x -> v]s)w) y a [y ->w][x->v]s. Esta transformación de funciones de “multiples argumentos” a funciones de orden superior es llamado currying.
tru = λt.λf.t
fls = λt.λf.f
Para representar los boleados, vamos a utilizar a las anteriores dos expresiones de tru y fls, para representar al verdadero y falso boleano, como no se tienen este tipo primitivo en el calculo lambda, como otras abstracciones, necesitamos de alguna modelar la misma en función de funciones lambda.
Luego con estos dos terminos lambda, podemos definir el resto de los operadores lógicos, mediante algunas formulaciones:
and = λp.λq.p q p
alternativa para describir al and en calculo λ:
and = λp.λq.p q fls
(Mostrar que ambas implementaciones funcionan bien...)
or = λp.λq.p p q
alternativa para describir la operacion or:
or = λp.λq.p tru q
(Mostrar que ambas implementaciones funcionan bien...)
not = λp.p fls tru
xor = λp.λq.p (not q) q
(Demostrar not y xor...)
Ahora veamos algunas operaciones adicionales como el if/then/else:
ifthenelse = λc.λt.λe.c t e
- test = λl. λm. λn. l m n
- test tru then else = (λl. λm. λn. l m n) (λt. λf. t)
- test fls then else = (λl. λm. λn. l m n) (λt. λf. f)
There are several possible ways to define the natural numbers in lambda calculus, but by far the most common are the Church numerals, which can be defined as follows:
0 := λs.λz.z
1 := λs.λz.s z
2 := λs.λz.s (s x)
3 := λs.λz.s (s (s z))
…
Un número de Church es una función de orden superior: toma una función de argumento único y devuelve otra función de argumento único. El número de Church n es una función que toma una función s como argumento y devuelve la enésima composición de s, es decir, la función está compuesta consigo misma n veces. Esto se denota s (n) y de hecho es la potencia número s de s(considerada como un operador); s (0) se define como la función de identidad. Tales composiciones repetidas (de una sola función) obedecen las leyes de los exponentes, por lo que estos números se pueden usar para la aritmética. (En el cálculo lambda original de Church, el parámetro formal de una expresión lambda debía aparecer al menos una vez en el cuerpo de la función, lo que hacía imposible la definición anterior de 0).
A la función s, se la conoce generalmente como la función sucesor o succ, que esta representada de la siguiente manera
succ = λn λs λz s (n s z)
Este termino toma un numero de Church n y retorna otro numeral de Church, es decir yieldea una función que toma un argumento s y z, y lo aplica repetidamente a z. Obtenemos el numero de aplicaciones correcta de s a z pasando primero antes estos dos argumentos (s y z) a n y luego aplicando una vez mas s sobre el resultado.
Debido a que la composición m-ésima de f compuesta con la composición n-ésima de f da la composición m + n-ésima de f, la adición se puede definir de la siguiente manera:
plus = λm.λn.λs.λz.m s (n s z)
Ahora podemos hacer algunas mezclas entre los números de Church y los booleans visto antes, para hacer una pregunta si es cero
Iszro = λm. m (λx. fls) tru
Vimos que un paso de la evaluación suele a veces reducir un poco mas nuestra expresión o hacer una o ninguna reducción. Hay casos puntuales que una reducción puede llegar a realizar resultados un tanto interesantes. Por ejemplo el combinador divergente omega
Omega = ( λ x . x x ) ( λ x . x x )
Contiene un solo redex, y reduciendo este resulta en la misma expresión inicial, a estos términos que se escapan y que carecen de forma normal, se dicen que divergen. A este combinador omega, tiene una generalización llamada combinador de punto fijo, que puede ser usado para definir funciones recursivas como el factorial
fix ≡ λf . (λx . f (λy x x y)) (λx . f (λy x x y)
Nota, a veces se lo muestra el combinado de punto fijo de la siguiente manera:
fix ≡ λ f . (λ x . f (x x)) (λ x . f (x x)))
Esta es la notación de call-by-name
A veces es mas difícil de explicar bien sobre su definición y lo mejor es hacer un ejemplo usándolo, para entender cual es su función.
Usando el fix de la nota, por simplicidad
fix g ≡ λf . (λx . f (x x)) (λx . f (x x))) g
≡ (λx . g (x x)) (λx . g (x x)))
≡ g (λx . g (x x)) (λx . g (x x)))
≡ g (λf . (λx . f (x x)) (λx . f (x x))) g
≡ g fix g
Aplicando repetidamente esta igualdad
fix g = g fix g = g (g( Y g)) = …
En el cálculo lambda, Y g es un punto fijo de g, debido a que expande a g (Y g). Ahora, para completar nuestra llamada recursiva a la función factorial, simplemente llamaría g (Y g) n, donde n es el número del cual queremos calcular el factorial.
Dado el siguiente ejemplo robado de wikipedia, y teniendo que fix = Y, por ejemplo n = 5, esta se expandirá como:
(λ n.(1, si n = 0; y n·((Y g)(n-1)), si n>0)) 5
1, si 5 = 0; y 5·(g(Y g)(5-1)), si 5>0
5·(g(Y g) 4)
5·(λ n. (1, si n = 0; y n·((Y g)(n-1)), si n>0) 4)
5·(1, si 4 = 0; y 4·(g(Y g)(4-1)), si 4>0)
5·(4·(g(Y g) 3))
5·(4·(λ n. (1, si n = 0; y n·((Y g)(n-1)), si n>0) 3))
5·(4·(1, if 3 = 0; y 3·(g(Y g)(3-1)), si 3>0))
5·(4·(3·(g(Y g) 2)))
Hay mucho mas para hablar sobre calculo lambda, o mas bien sobre como expandir al calculo con varias funciones, por ahora vamos a centrarnos en solamente entender las formalidades de lo que vimos ahora y un par de reglas mas antes de pasar al proximo tema.
Un ejemplo completo con reducciones α y β
(λz.z) ((λy.y y) (λx.x a)) aplicamos β-reducción (donde y, reemplazo con (λx.x a))
(λz.z) ((λx.x a) (λx.x a)) aplicamos β-reducción (donde x, reemplazo con (λx.x a))
(λz.z) ((λx.x a) a) aplicamos β-reducción (donde x, reemplazo con a)
(λz.z) (a a) aplicamos α-reducción (renombro z por a)
a a resultado
A continuation vamos a definir formalmente el calculo lambda para terminar de redondear un poco la idea de esta parte
-
t = x / x ∈ Var
-
t = λx.M / x ∈ Var y N es una expresion lambda
-
t = (MN) / M and N son expresiones lambda
Tipos de expresiones en calculo lambda
- variables (referencing expresiones lambda)
- Abstracciones lambda (definen funciones)
- applicaciones (invocan funciones)
Para las conversiones
M →α N La regla aplica de izquierda a derecha
M ←α N La regla aplica de derecha a izquierda
M ↔α N La regla de conversion aplica a ambos sentidos
Para substituciones
M[x→N] x en M es sustituido por N
M[x←N] N en M es sustituido por x
M[x↔N] x en M es sustituido por N o N en M es sustituido por x dependiendo de la direccion de la conversion
Hasta ahora no vimos esto pero la conversion alpha nos permite cambiar el nombre de una variable ligada a una función
λx.M →α λx0.M[x → x0] 1
where x0 is not allowed to be a free variable in M. The process of alpha conversion may not alter the value of the expression. The expression to be converted (M) and the converted result (N) are said to be equal modulo alpha: M =α N.
The following transformation is called β-conversion:
((λx.M)N) ↔β M[x ↔ N]
β-Conversion primarily consists of the process of substituting a bound variable in the body of a lambda abstraction by the argument passed to the function whenever it is applied. This process is called β-reduction.
Reducible Expression ‘redex’ β-reduction can be applied only to reducible expressions. A reducible expression called ‘redex’ for short is defined as follows:
((λx.M)N)
El proceso inverso de convertir una expresión lambda reducida por medio de β-reduction a la expresión reducible es otro aspecto de la conversion β, llamada β-abstraction
+ 4 1 ← (λx . + x 1) 4
Por lo que esta expresión resume la abstracción alpha:
((λx.M)N) ←β M[x ← N]
Ejemplos
((λx.x x)(λy.y)) →β ((λy.y)(λy.y)) →β (λy.y)
((λx.(λy.x y))y) →β (λy’.y y’)
Observación: El segundo ejemplo demuestra la necesidad de la conversión alfa. La variable unida a lambda y tuvo que cambiarse de nombre y’, para evitar la captura de la y libre (resultante de la sustitución de x por y en el cuerpo de la primera abstracción de lambda) por la segunda lambda.
Al igual que la conversión β, la conversión η se puede realizar de izquierda a derecha y de derecha a izquierda y, por lo tanto, se subdivide en reducción de Eta y abstracción
η-conversion es otro tipo de conversion que deja sin cambiar la semántica de una expresión lambda:
Formalmente se define de esta manera:
(λx.Mx) ↔η M ,
Y un ejemplo podría ser
(λx . + 1 x) ↔η (+ 1)
La η-reduction es útil para eliminar abstracciones lambda redundantes. La siguiente regla puede ser interpretada de la siguiente manera:
Si el único propósito de una abstracción lambda es pasar su argumento a otra función, entonces la abstracción lambda es redundante y puede eliminarse mediante la η-reduction.
En un entorno donde se utiliza la "evaluación eager" como en Scheme, tales abstracciones lambda redundantes se utilizan como un wrapper alrededor de una expresión lambda para evitar una evaluación inmediata. Se resume la η-reduction de la siguiente manera
(λx.Mx) →η M ,
Donde x no seria una variable libre en M
Un simple ejemplo seria
(λx . F x) ↔η F
La abstraction eta por otro lado es util en lenguajes eager para crear un wrapper alrededor de una expresión lambda, en lenguajes de evaluación lazy, las transformaciones eta son utilizados en el mismo compilador. La forma genérica de la abstracción eta es:
(λx.Mx) ←η M
La idea de De Bruijn es que se pudisen representar los términos de una manera mucho mas directa, y a veces menos intuitiva, reemplazando las variables de una función que se representan de manera nominativa por un numero al que la variable apunta directamente al contexto con el que esta bindeado o ligado. Esto se hace reemplazando por numeros , donde el numero k significa la variable bindeada con la clausa lambda que esta a k contextos, por ej. Sobre el termino simple λx. x eso se puede representar como λ.1 mientras que λx. λy. x (y x) pertenece a λ λ 2 (1 2).
A veces hay autores que prefieren partir del 0 o del 1. Los términos sin nombre se denominan a veces términos De Bruijn, y las variables numéricas indices De Bruijn. Los compiladores usan el termino “distancia estatica” para representar el mismo concepto,
Un ejemplo mas gráfico.. robado de wikipedia sin vergüenza es el siguiente
Para la expresion lambda λz. (λy. y (λx. x)) (λx. z x) la misma pasada a indices De Bruijn es λ (λ 1 (λ 1)) (λ 2 1). Veamos visualmente como es
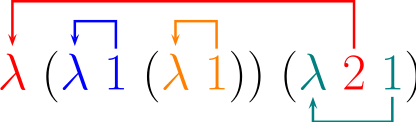
Los términos usando estos indices se escriben de la siguiente manera
M, N, … ::= n | M N | λ M
Donde n pertenece a los números naturales mayores a 0 y pertenecen a las variables. Una variable esta en el scope si al menos tiene n contextos bindeados (λ), de otra manera es libre. El lugar para bindear una variable n es la _n_th clausula que esta en el contexto a partir del contexto mas interno.
La operación mas primitiva en los términos lambda es la sustitución, reemplazando las variables libres con otros términos, por lo que en una reducción beta, deberíamos hacer:
- Buscar las instancias de las variables n1, n2, …, nk en M que estan bindeadas por λ en λ M,
- Decrementar las variables libres de M para matchear la bindeo externo de λ
- Reemplazar n1, n2, …, nk con N, incrementando la cantidad de variables libre que se han encontrado en N cada vez, para matchear el numero de contextos lambda, bajo el cual la variable correspondiente ocurre cuando N sustituye por uno de los ni.
El chequeo de tipos simple para calculo lambda es una técnica para probar propiedades simples, y a diferencia de otras tecnicas de prueba de teoremas y pruebas basados en semántica axiomática, la verificación de tipos por lo general no puede determinar que el resultado sea correcto. Por lo que es una forma de probar si se trata de un programa bien formado que satisface ciertas propiedades deseables. Los sistemas de tipos son una técnica poderosa. Los investigadores han descubierto cómo usar el tipo Sistemas para una variedad de diferentes tareas de verificación. Lo que veremos brevemente es la primera impresion del sistema de tipos sobre calculo lambda.
En si esta variacion tipada es relativamente simple, ya que no se introduce nada nuevo sobre la idea del calculo lambda, porque al ser un complemento de este es mas bien un chequeo de tipos y no mucho mas, ya que el calculo lambda no fue pensado para soportar tipos. Por lo que las reglas de sustitucion y como se forman los terminos no es algo que se vera afectado, como veremos mas adelante, en el codigo. Para empezar, un termino lambda es considerado bien si un tipo puede ser derivado de el usando reglas, y le dareos semanticas operaciones y denotacionales para este lenguaje.
Para empezar vamos a definir los tipos primitivos, que no se relacionan en principio con los terminos de las expresiones lambda.
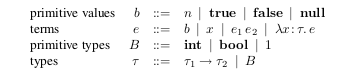
Vemos que los tipos y las construcciones de las expresiones lambda no se relaciona, sino que el sistema de tipos sera el que tenga la tarea de correlacionar estos dos modelos, por un lado el modelo de los tipos de datos y por el otro el del modelo del lenguaje intermedio que modela las expresiones del calculo lambda. Laotra diferencia es que la abstraccion lambda explicita menciona el tipo de sus argumentos. Un valor puede ser un numero, un booleano, nulo o una abstraccion cerrada λx : τ. e. El conjunto de valores esta denotado por Val. El conjuntos de tipos esta denotado por Type. Hay un conjunto de reglas de tipado, donde se pueden asociar un tipo con una estructura. Si un tipo τ puede ser derivado para un termino/estructura e de acuerdo a las reglas de tipado, lo deberiamos escribir como
e : τ
Esto es lo que de conoce como un juicio de tipo (type judgement)
Por ejemplo, cada numero tiene un tipo int, por lo que 3: int. El tipo nulo es unico y ninguno mas posee su tipo. La funcion
TRUE int = λx : int. λy : int. x tiene la firma int → (int → int)
El constructor asocia a la dierecha por lo que int → (int → int) is the same as int → int → int
Por lo que se puede llegar a la conclusion de:
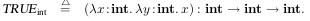
No todos los terminos lambda pueden ser considerados validos por el sistema de tipo, por ej
(λx : int. x x) and (true 3)
Este caso es un caso de un codigo mal formado, y es considerado invalido. Por ahora no nos vamos a detener como hacer la coercion de tipos sobre funciones mas compejas, sino a explicar el tipado simple.
Las reglas de tipado determinaran si los terminos que se ingresan son programas lambdas validos. Son un conjunto de reglas que permiten la derivacion de juicio de tipos, de la forma
Γ ` e : τ
Γ es nuestro entorno de tipos, que la forma mas simple es un mapa con las variables nominales o ids que estan asociadas a los tipos, y que se usan para determinar los tipos de variables libres en e. El dominio de Γ es una funcion parcion Var * Type es denotado como dom(Γ).
El se obtiene el entorno Γ[x 7→ τ ], rebindeando la variable x a τ (o creando un nuevo binding si x 6∈ dom(Γ)):
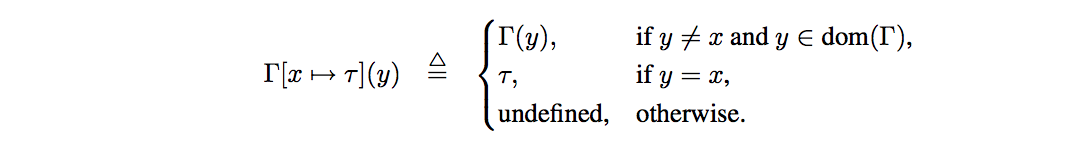
La notacion Γ, x : τ es sinonimo con Γ[x 7→ τ ], donde el primero es la notacion que se ve en gral en bibliografia. Tambien se ve a veces la notacion x : τ ∈ Γ que significa Γ(x) = τ
Tambien escribimos Γ ' e : τ para expesar que el juicio de tipo es derivado de las reglas de tipado definidas. El entorno ø es el entorno vacio, y el juicio ' e : τ es en realidad ø ' e : τ
Las reglas de tipo son:
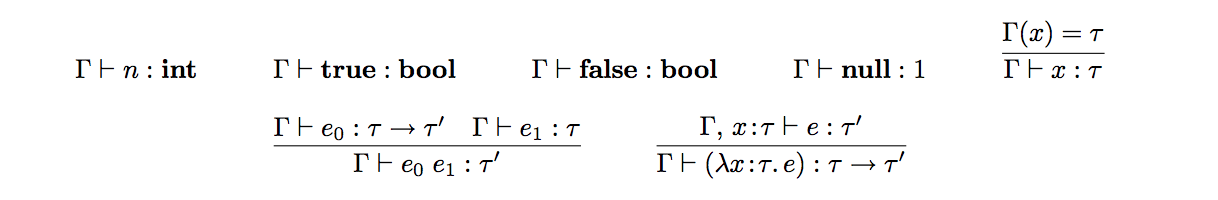
Vamos a explicar brevemente cada una de las reglas de tipado
- Las primeras cuatro reglas son para definir que los valores bases poseen sus propios tipos bases
- Para una variable x, Γ ` x : τ explicita que el binding x : τ aparece en el entorno Γ, por lo que se fija lo siguiente: Γ(x) = τ
- Una aplicacion e0 e1 representa el resultado de aplicar la funcion representado por e0 al argumento representado por e1, por lo que para τ0, e0 debe ser una funcion del tipo τ → τ0 para un τ0, y su argumento e1 debe ser del tipo τ. Esto es capturado por esta regla.
- Finalmente una abstraccion λx : τ. e, representa una funcion. El tipo de entrada (argumento) que debe matchear con la anotacion del termino, por lo que el tipo de la funcion debe ser τ → τ0 para un τ0. El tipo τ0 del resultado es el tipo de cuerpo y que posee la suposicion extra del tipo x: τ.
Cada termino bien tipado tiene un arbol de prueba que consiste en las aplicaciones del tipo de reglas de derivacion de un tipo para la expresion. Podemos chequear el tipo de un termino construyendo su arbol de prueba. Por ejemplo, veamos esta expresion lambda
(λx : int. λy : bool. x) 2 true
que evalua finalmente a 2. Desde que 2: Int esperamos que se cumpla
((λx : int. λy : bool. x) 2 true) : int
Veamos un poco como se puede probar esto

Un chequeador de tipos automatico puede construir arboles de pruebas como este para testear si el programa esta bien tipado o no. Una razon importante para esto sea posible es que las reglas son orientadas a la sintaxis, por lo que hay solo una regla de tipos que aplica a una forma dada de e. Por lo que no hay que realizar busquedas para construir un arbol de prueba. Para este sistema de tipos, los tipos, si existen son unicos. Por lo que si
Γ ` e : τ
y
Γ ` e : τ0
entonces
τ = τ0
Esto puede ser probado simple por medio de induccion estructural
Hay un gran problema con el tipado simple y es que perdemos la expresividad del calculo lambda, sobre funciones que se componen arbitrariamente, ya que pueden tener tipos que no necesariamente se matcheen. Lo mas importante es que perdemos la capacidad de escribir loops o funciones recursivas como vimos antes con la funcion omega:
Omega = ( λ x . x x ) ( λ x . x x )
Veamos que no podemos ahora hacer tipar algo como λx : σ. xx
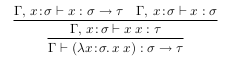
Podemos ver que tenemos que cumplir tanto con
Γ, x : σ ` x : σ → τ
Γ, x : σ ` x : σ
Sin embargo, desde que los tipos son unicos, esto es imposible, por lo que no podemos tener σ = σ → τ, y tampoco podemos hacer que una expresion de un tipo pueda ser una subexpresion de el mismo, entonces tenemos que llegar a la conclusion de que no se puede tipar. Esto es una gran limitante del sistema simple de tipado, pero hay otros tipados mas avanzados, llamados de segundo orden que restauran la posibilidad de tener funciones recursivas y loops.