Skip to content

Latest commit

 

History

History
80 lines (59 loc) · 2.83 KB

readme.md

File metadata and controls

80 lines (59 loc) · 2.83 KB
Raw

212. Word Search II

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

e1

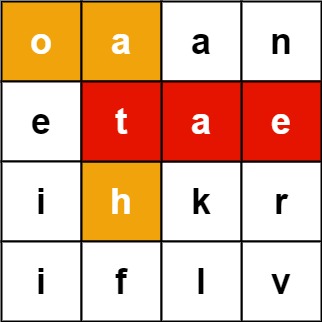
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"] Output: ["eat","oath"]

Example 2:

e2

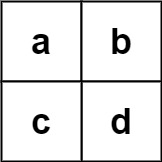
Input: board = [["a","b"],["c","d"]], words = ["abcb"] Output: []

Constraints:

  • m == board.length
  • n == board[i].length
  • 1 <= m, n <= 12
  • board[i][j] is a lowercase English letter.
  • 1 <= words.length <= 3 * 104
  • 1 <= words[i].length <= 10
  • words[i] consists of lowercase English letters.
  • All the strings of words are unique.

Solution

class TrieNode:
    def __init__(self):
        self.children = {}
        self.isEnd = False
        self.word = None

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        root = TrieNode()
        for word in words:
            node = root
            for char in word:
                if char not in node.children:
                    node.children[char] = TrieNode()
                node = node.children[char]
            node.isEnd = True
            node.word = word

        def dfs(row, col, node):
            if node.isEnd:
                result.add(node.word)
            if 0 <= row < len(board) and 0 <= col < len(board[0]) and board[row][col] in node.children:
                char = board[row][col]
                board[row][col] = '#'  # Mark as visited
                for dr, dc in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
                    dfs(row + dr, col + dc, node.children[char])
                board[row][col] = char  # Backtrack

        result = set()
        for row in range(len(board)):
            for col in range(len(board[0])):
                if board[row][col] in root.children:
                    dfs(row, col, root)
        return list(result)

Thoughts

Time Complexity

The time complexity is O(M * N * 4^L), where M and N are the dimensions of the board, and L is the maximum length of the words. This is because, for each cell, we perform a DFS with 4 possible directions, and the maximum depth of the DFS is the length of the longest word.

Space Complexity

The space complexity is O(W * L) for the trie, where W is the number of words and L is the maximum length of the words. Additionally, the space required for the recursion stack in the DFS is O(M * N) in the worst case.