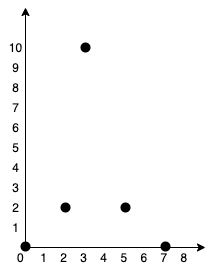
You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
Example 1:
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation:

Example 2:
Input: points = [[3,12],[-2,5],[-4,1]] Output: 18
1 <= points.length <= 1000-106 <= xi, yi <= 106- All pairs
(xi, yi)are distinct.
import heapq
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
def manhattan_distance(p1, p2):
return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])
n = len(points)
total_cost = 0
visited = set([0])
min_heap = [(manhattan_distance(points[0], points[i]), i) for i in range(1, n)]
heapq.heapify(min_heap)
while len(visited) < n:
cost, point = heapq.heappop(min_heap)
if point in visited:
continue
visited.add(point)
total_cost += cost
for i in range(n):
if i not in visited:
heapq.heappush(min_heap, (manhattan_distance(points[point], points[i]), i))
return total_costCan use Prim's algorithm or Kruskal's algorithm to find the Minimum Spanning Tree (MST) of the graph. Review those concepts.
The time complexity is O(N^2 log N), where N is the number of points. This is because, in the worst case, we need to push and pop each edge (N^2 edges) in the min-heap, and each heap operation takes O(log N) time.
The space complexity is O(N) for the min-heap and the visited set.