A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node's values in the path.
Given the root of a binary tree, return the maximum path sum of any non-empty path.
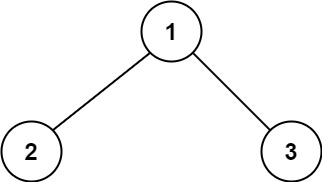
Example 1:
Input: root = [1,2,3] Output: 6 Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
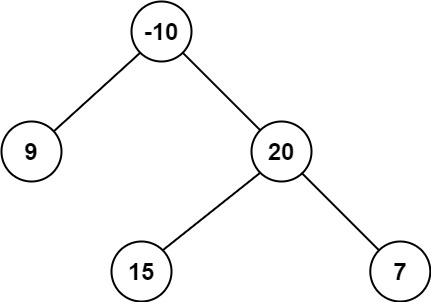
Example 2:
Input: root = [-10,9,20,null,null,15,7] Output: 42 Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Constraints:
- The number of nodes in the tree is in the range
[1, 3 * 104]. -1000 <= Node.val <= 1000
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def maxPathSum(self, root: TreeNode) -> int:
def helper(node):
if not node:
return 0
# Recursively calculate the maximum path sum for the left and right subtrees
left = max(helper(node.left), 0)
right = max(helper(node.right), 0)
# Update the global maximum path sum
self.max_sum = max(self.max_sum, node.val + left + right)
# Return the maximum path sum that can be extended to the node's parent
return node.val + max(left, right)
self.max_sum = float('-inf')
helper(root)
return self.max_sum
The time complexity of this solution is O(n), where n is the number of nodes in the tree. This is because we visit each node exactly once during the recursion.
The space complexity of this solution is O(h), where h is the height of the tree. This is because the maximum amount of space utilized by the recursion stack would be equal to the height of the tree. In the worst case, the tree is a linear chain (i.e., each node has only one child), and the height of the tree is O(n). In the best case, the tree is completely balanced, and the height of the tree is O(log n).