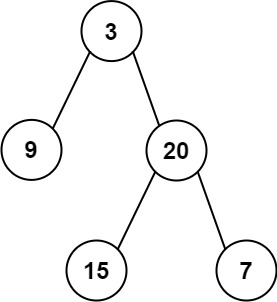
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
Example 1:
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
Example 2:
Input: preorder = [-1], inorder = [-1] Output: [-1]
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorderandinorderconsist of unique values.- Each value of
inorderalso appears inpreorder. preorderis guaranteed to be the preorder traversal of the tree.inorderis guaranteed to be the inorder traversal of the tree.
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
if not preorder or not inorder:
return None
# The first element of preorder is the root
root = TreeNode(preorder[0])
# Find the index of the root in inorder list
mid = inorder.index(preorder[0])
# Recursively construct the left and right subtrees
root.left = self.buildTree(preorder[1:mid+1], inorder[:mid])
root.right = self.buildTree(preorder[mid+1:], inorder[mid+1:])
return rootThe recursive construction preorder indices are pretty confusing, need to revise.
The time complexity of this solution is O(n^2) in the worst case, where n is the number of nodes in the tree. This is because for each node, we are searching for its index in the inorder list, which takes O(n) time. In the best case, if the tree is balanced, the time complexity can be reduced to O(n log n).
The space complexity of this solution is O(n), where n is the number of nodes in the tree. This is because we are storing the entire tree in memory. Additionally, the recursion stack will also use space, but its size will be at most the height of the tree, which is O(log n) in the best case (balanced tree) and O(n) in the worst case (skewed tree).