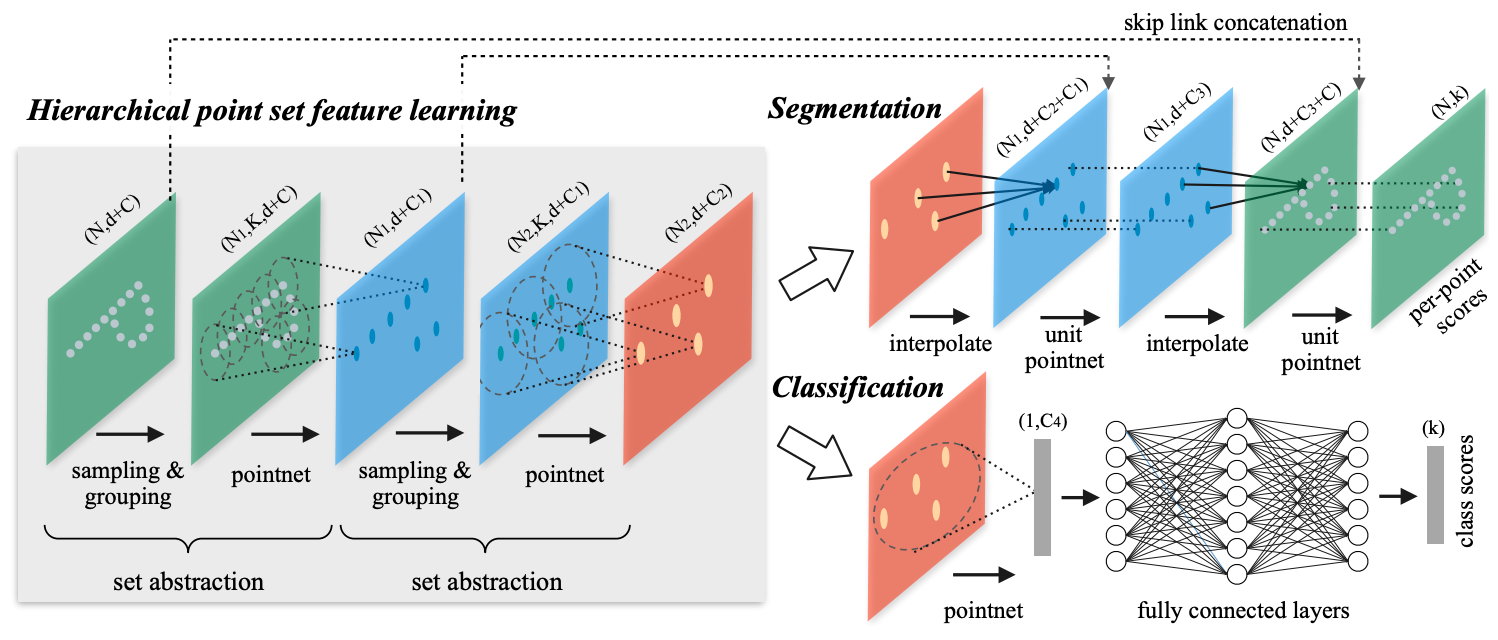
PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space
Few prior works study deep learning on point sets. PointNet by Qi et al. is a pioneer in this direction. However, by design PointNet does not capture local structures induced by the metric space points live in, limiting its ability to recognize fine-grained patterns and generalizability to complex scenes. In this work, we introduce a hierarchical neural network that applies PointNet recursively on a nested partitioning of the input point set. By exploiting metric space distances, our network is able to learn local features with increasing contextual scales. With further observation that point sets are usually sampled with varying densities, which results in greatly decreased performance for networks trained on uniform densities, we propose novel set learning layers to adaptively combine features from multiple scales. Experiments show that our network called PointNet++ is able to learn deep point set features efficiently and robustly. In particular, results significantly better than state-of-the-art have been obtained on challenging benchmarks of 3D point clouds.
We implement PointNet++ and provide the result and checkpoints on ScanNet and S3DIS datasets.
Notice: The original PointNet++ paper used step learning rate schedule. We discovered that cosine schedule achieves much better results and adopt it in our implementations. We also use a larger weight_decay factor because we find it consistently improves the performance.
| Method | Input | Lr schd | Mem (GB) | Inf time (fps) | mIoU (Val set) | mIoU (Test set) | Download |
|---|---|---|---|---|---|---|---|
| PointNet++ (SSG) | XYZ | cosine 200e | 1.9 | 53.91 | model | log | ||
| PointNet++ (SSG) | XYZ+Color | cosine 200e | 1.9 | 54.44 | model | log | ||
| PointNet++ (MSG) | XYZ | cosine 250e | 2.4 | 54.26 | model | log | ||
| PointNet++ (MSG) | XYZ+Color | cosine 250e | 2.4 | 55.05 | model | log |
Notes:
-
The original PointNet++ paper conducted experiments on the ScanNet V1 dataset, while later point cloud segmentor papers often used ScanNet V2. Following common practice, we report results on the ScanNet V2 dataset.
-
Since ScanNet dataset doesn't provide ground-truth labels for the test set, users can only evaluate test set performance by submitting to its online benchmark website. However, users are only allowed to submit once every two weeks. Therefore, we currently report val set mIoU. Test set performance may be added in the future.
-
To generate submission file for ScanNet online benchmark, you need to modify the ScanNet dataset's config. Change
ann_file=data_root + 'scannet_infos_val.pkl'toann_file=data_root + 'scannet_infos_test.pkl', and then simply run:python tools/test.py ${CONFIG_FILE} ${CHECKPOINT_FILE} --format-only --options 'txt_prefix=exps/pointnet2_scannet_results'
This will save the prediction results as
txtfiles inexps/pointnet2_scannet_results/. Then, go to this folder and zip all files intopn2_scannet.zip. Now you can submit it to the online benchmark and wait for the test set result. More instructions can be found at their official website.
| Method | Split | Lr schd | Mem (GB) | Inf time (fps) | mIoU (Val set) | Download |
|---|---|---|---|---|---|---|
| PointNet++ (SSG) | Area_5 | cosine 50e | 3.6 | 56.93 | model | log | |
| PointNet++ (MSG) | Area_5 | cosine 80e | 3.6 | 58.04 | model | log |
Notes:
- We use XYZ+Color+Normalized_XYZ as input in all the experiments on S3DIS datasets.
Area_5Split means training the model on Area_1, 2, 3, 4, 6 and testing on Area_5.
Since PointNet++ testing adopts sliding patch inference which involves random point sampling, and the test script uses fixed random seeds while the random seeds of validation in training are not fixed, the test results may be slightly different from the results reported above.
@inproceedings{qi2017pointnet++,
title={PointNet++ deep hierarchical feature learning on point sets in a metric space},
author={Qi, Charles R and Yi, Li and Su, Hao and Guibas, Leonidas J},
booktitle={Proceedings of the 31st International Conference on Neural Information Processing Systems},
pages={5105--5114},
year={2017}
}