0040.md

40. 组合总和 II

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

所有数字（包括目标数）都是正整数。 解集不能包含重复的组合。

示例 1：

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2：

输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
  [1,2,2],
  [5]
]

分析阶段

这一题与39. 组合总和相似，最大的不同在于：数组中存在重复元素，但不能重复使用。

1、问题类型

第二类：对某种数结构和算法的使用

使用的算法：在给定的元素集合中，找到满足条件的组合，使用“回溯算法“

数据结构：回溯算法需要构建空间状态树，使用树结构

2、解题思路

“回溯算法”要确定以下条件，然后构建出解集的空间状态树。

（1）选择列表

给定的数组就是选择列表，与前面相同，为了减少递归层次，先把数组排序。

（2）路径

记录已经选择的元素值，以及当前路径中所有元素和值与 target 的差值。

（3）结束条件

达到什么条件时结束结束当前节点的遍历？

• 路径中所有元素值与 target 的差值小于等于0：
  • 小于0，当前路径无效
  • 等于0，把路径添加到结果集

（4）选择

什么条件下才把当前元素添加进路径中？

因为每个元素只能使用一次，所以在遍历数组时，要跳过当前元素。

另外，存在重复元素但不允许重复路径，因此在选择元素时，要判断是否与前一个元素相等（数组是有序的），如果相等就跳过，不相等才添加进路径。

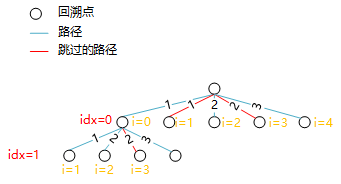
这里会引起另一个问题，如下面的“空间状态树”所示，图中 $candidates = [1,1,2,2,3]$，idx 表示当前递归的层次，i 表示当前选择路径上元素所在的下标：

从图中可以看出：

1、当idx = 0 时，i = 1、i = 3的路径是无效的，因为 $candidates[i-1] == candidates[i]$

2、当idx = 1 时，虽然都满足条件 $candidates[i-1] == candidates[i]$，但是i = 1的路径是有效的，i = 3的路径是无效的

3、也就是说，如果相等的两个元素在同一层的递归中，那么就要跳过第二个元素

怎么判断相等的两个元素是否在同一层递归中？

如果满足条件 $candidates[i-1] == candidates[i]$，要根据 idx 的值进行判断：

• $idx == 0$，这两个元素都在一层递归中，跳过
• $idx != 0$，如果$ i - 1 == idx - 1$，说明这两个元素不在同一层递归中，可以添加进路径中

这部分代码判断如下：

if (i > 0 && candidates[i - 1] == candidates[i]) {
    if (idx == 0) {
        continue;
    } else {
        if (i - 1 != idx - 1) {
            continue;
        }
    }
}

每层递归开始时，只有第一个元素会和上一层做比较，因此可以通过比较 i 和 idx 的值来简化上面的判断。

最外层条件$ i > 0$，第一个内层条件是：$idx == 0$，导致 $i != idx$；第二个内层条件是：$i - 1 != idx - 1$，也导致 $ i != idx$，因此可以简化成：

if(i != idx && candidates[i - 1] == candidates[i]) {
    continue;
}

编码阶段

class Solution {

    public static void main(String[] args) {
        int[] candidates = new int[]{10, 1, 2, 7, 6, 1, 5};
        int target = 8;
        System.out.println("=======" + new Solution().combinationSum2(candidates, target));
    }

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> res = new ArrayList<>();

        List<Integer> path = new ArrayList<>();

        backtrack(res, path, candidates, target, 0);
        return res;
    }

    /**
     * 回溯递归
     *
     * @param res        结果集
     * @param path       路径
     * @param candidates 选择列表
     * @param diff       与目标值的差值
     * @param idx        当前遍历的元素下标
     */
    public void backtrack(List<List<Integer>> res, List<Integer> path, int[] candidates, int diff, int idx) {
        if (diff == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        if (diff < 0) {
            return;
        }

        for (int i = idx; i < candidates.length; i++) {
            if (diff - candidates[i] < 0) {
                // 结束遍历
                break;
            }
            // 选择判断
            if(i != idx && candidates[i - 1] == candidates[i]) {
                continue;
            }

            path.add(candidates[i]);
            backtrack(res, path, candidates, diff - candidates[i], i + 1);

            path.remove(path.size() - 1);
        }
    }
}

总结阶段

1、通过排序来减少递归层次，并跳过重复的元素

2、递归会造成重复的元素在不同层次上，要做特殊判断