给定一个 m x n 二进制数组表示的网格 grid ,一个岛屿由 四连通 (上、下、左、右四个方向)的 1 组成(代表陆地)。你可以认为网格的四周被海水包围。
如果两个岛屿的形状相同,或者通过旋转(顺时针旋转 90°,180°,270°)、翻转(左右翻转、上下翻转)后形状相同,那么就认为这两个岛屿是相同的。
返回 这个网格中形状 不同 的岛屿的数量 。
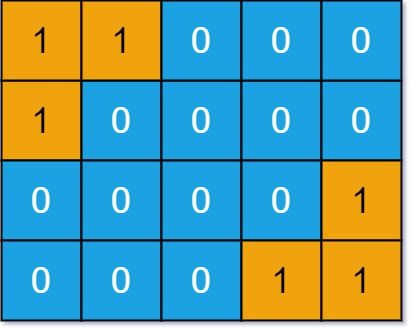
示例 1:
输入: grid = [[1,1,0,0,0],[1,0,0,0,0],[0,0,0,0,1],[0,0,0,1,1]] 输出: 1 解释: 这两个是相同的岛屿。因为我们通过 180° 旋转第一个岛屿,两个岛屿的形状相同。
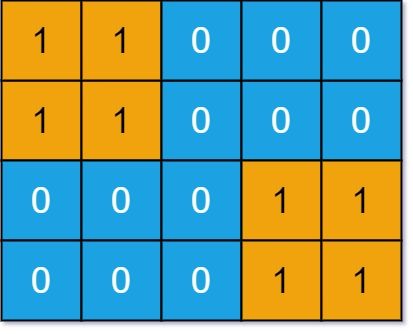
示例 2:
输入: grid = [[1,1,0,0,0],[1,1,0,0,0],[0,0,0,1,1],[0,0,0,1,1]] 输出: 1
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]不是0就是1.
先利用 DFS 找出每个岛屿,随后对岛屿进行翻转、旋转等操作,得到以下 8 种不同的情况,并对这些情况进行标准化 normalize 处理,得到该岛屿的特征值,放到哈希表中。最后返回哈希表的元素数量即可。
原坐标: (i, j)
上下翻转: (i, -j)
左右翻转: (-i, j)
90°旋转: (j, -i)
180°旋转: (-i, -j)
270°旋转: (-j, -i)
90°旋转+左右翻转: (-j, -i)
90°旋转+上下翻转: (j, i)
标准化 normalize 的思路是:对于岛屿的每一种情况,先按照横、纵坐标升序排列坐标点,得到的第一个点 (a, b) 是最小的点,将其化为 (0, 0),对于其他点 (x, y),则化为 (x - a, y - b)。然后排序这 8 种情况,获取最小的一种,作为该岛屿的标准化值。
class Solution:
def numDistinctIslands2(self, grid: List[List[int]]) -> int:
def dfs(i, j, shape):
shape.append([i, j])
grid[i][j] = 0
for a, b in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
x, y = i + a, j + b
if 0 <= x < m and 0 <= y < n and grid[x][y] == 1:
dfs(x, y, shape)
def normalize(shape):
shapes = [[] for _ in range(8)]
for i, j in shape:
shapes[0].append([i, j])
shapes[1].append([i, -j])
shapes[2].append([-i, j])
shapes[3].append([-i, -j])
shapes[4].append([j, i])
shapes[5].append([j, -i])
shapes[6].append([-j, i])
shapes[7].append([-j, -i])
for e in shapes:
e.sort()
for i in range(len(e) - 1, -1, -1):
e[i][0] -= e[0][0]
e[i][1] -= e[0][1]
shapes.sort()
return tuple(tuple(e) for e in shapes[0])
m, n = len(grid), len(grid[0])
s = set()
for i in range(m):
for j in range(n):
if grid[i][j]:
shape = []
dfs(i, j, shape)
s.add(normalize(shape))
return len(s)class Solution {
private int m;
private int n;
private int[][] grid;
public int numDistinctIslands2(int[][] grid) {
m = grid.length;
n = grid[0].length;
this.grid = grid;
Set<List<List<Integer>>> s = new HashSet<>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
List<Integer> shape = new ArrayList<>();
dfs(i, j, shape);
s.add(normalize(shape));
}
}
}
return s.size();
}
private List<List<Integer>> normalize(List<Integer> shape) {
List<int[]>[] shapes = new List[8];
for (int i = 0; i < 8; ++i) {
shapes[i] = new ArrayList<>();
}
for (int e : shape) {
int i = e / n;
int j = e % n;
shapes[0].add(new int[] {i, j});
shapes[1].add(new int[] {i, -j});
shapes[2].add(new int[] {-i, j});
shapes[3].add(new int[] {-i, -j});
shapes[4].add(new int[] {j, i});
shapes[5].add(new int[] {j, -i});
shapes[6].add(new int[] {-j, i});
shapes[7].add(new int[] {-j, -i});
}
for (List<int[]> e : shapes) {
e.sort((a, b) -> {
int i1 = a[0];
int j1 = a[1];
int i2 = b[0];
int j2 = b[1];
if (i1 == i2) {
return j1 - j2;
}
return i1 - i2;
});
int a = e.get(0)[0];
int b = e.get(0)[1];
for (int k = e.size() - 1; k >= 0; --k) {
int i = e.get(k)[0];
int j = e.get(k)[1];
e.set(k, new int[] {i - a, j - b});
}
}
Arrays.sort(shapes, (a, b) -> {
for (int k = 0; k < a.size(); ++k) {
int i1 = a.get(k)[0];
int j1 = a.get(k)[1];
int i2 = b.get(k)[0];
int j2 = b.get(k)[1];
if (i1 != i2) {
return i1 - i2;
}
if (j1 != j2) {
return j1 - j2;
}
}
return 0;
});
List<List<Integer>> ans = new ArrayList<>();
for (int[] e : shapes[0]) {
ans.add(Arrays.asList(e[0], e[1]));
}
return ans;
}
private void dfs(int i, int j, List<Integer> shape) {
shape.add(i * n + j);
grid[i][j] = 0;
int[] dirs = {-1, 0, 1, 0, -1};
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k];
int y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
dfs(x, y, shape);
}
}
}
}typedef pair<int, int> PII;
class Solution {
public:
int numDistinctIslands2(vector<vector<int>>& grid) {
set<vector<PII>> s;
for (int i = 0; i < grid.size(); ++i) {
for (int j = 0; j < grid[0].size(); ++j) {
if (grid[i][j]) {
vector<PII> shape;
dfs(i, j, grid, shape);
s.insert(normalize(shape));
}
}
}
return s.size();
}
vector<PII> normalize(vector<PII>& shape) {
vector<vector<PII>> shapes(8);
for (auto& e : shape) {
int i = e.first, j = e.second;
shapes[0].push_back({i, j});
shapes[1].push_back({i, -j});
shapes[2].push_back({-i, j});
shapes[3].push_back({-i, -j});
shapes[4].push_back({j, i});
shapes[5].push_back({j, -i});
shapes[6].push_back({-j, -i});
shapes[7].push_back({-j, i});
}
for (auto& e : shapes) {
sort(e.begin(), e.end());
for (int k = e.size() - 1; k >= 0; --k) {
e[k].first -= e[0].first;
e[k].second -= e[0].second;
}
}
sort(shapes.begin(), shapes.end());
return shapes[0];
}
void dfs(int i, int j, vector<vector<int>>& grid, vector<PII>& shape) {
shape.push_back({i, j});
grid[i][j] = 0;
vector<int> dirs = {-1, 0, 1, 0, -1};
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < grid.size() && y >= 0 && y < grid[0].size() && grid[x][y] == 1)
dfs(x, y, grid, shape);
}
}
};