Khoảng cách Levenshtein là một chỉ số chuỗi cho đo lường sự khác biệt của hai chuỗi tuần tự. Nói gần gũi, khoảng cách Levenshtein giữa hai từ là số ký tự tối thiểu cần chỉnh sửa (chèn, xoá hoặc thay thế) để thay đổi một từ thành từ còn lại.
Trong toán học, khoảng cách Levenshtein giữa hai chuỗi a và b (có độ dài tương ứng là |a| và |b|) được cho bởi
với 
0 khi 
1 và ngược lại.
Và 
i của a và ký tự đầu tiên j của b.
Lưu ý phần tử đầu tiên ở mức tối thiểu tương ứng với xóa (từ a đến b), thứ hai đề chèn và thứ ba để ứng hoặc không ứng, tùy thuộc vào việc các ký hiệu tương ứng có giống nhau hay không.
Ví dụ, khoảng cách Levenshtein giữa kitten và sitting là 3, vì có 3 sửa đổi để một cái thành cái còn lại. Và không có cách nào để làm điều đó ít hơn 3 chỉnh sửa:
kitten → sitten (thay thế "s" cho "k")
sitten → sittin (thay thế "i" cho "e")
sittin → sitting (chèn "g" vào cuối).
Điều này có một loạt các ứng dụng, chẳng hạn như trình kiểm tra chính tả, hệ thống sửa lỗi để nhận dạng ký tự quang học, tìm kiếm chuỗi mờ và phần mềm hỗ trợ dịch ngôn ngữ tự nhiên dựa trên bộ nhớ dịch.
Bắt đầu với một ví dụ đơn giản cho tìm kiếm khoảng cách chỉnh sửa tối thiểu giữa chuỗi ME và MY. Trực giản bạn biết khoảng cách chỉnh sửa tối thiểu ở đây là 1, chỉ thay đổi E với Y. Nhưng cần hình thức hoá thuật toán theo một trật tự để có thể làm các việc phức tạp hơn ví dụ như chuyển đổi Saturday thành Sunday.
Để áp dụng công thức toán học tập trung vào chuyển đổi ME → MY bạn cần biết khoảng cách chỉnh sửa tối thiểu của chuyển đổi ME → M, M → MY và M → M trước.
Sau đó, bạn sẽ cần chọn một giá trị nhỏ nhất và thêm một thao tác để biến đổi các chữ cái cuối cùng là E → Y. Vì vậy, khoảng cách chỉnh sửa tối thiểu của phép biến đổi ME → MY đang được tính toán dựa trên ba phép biến đổi có thể có trước đó.
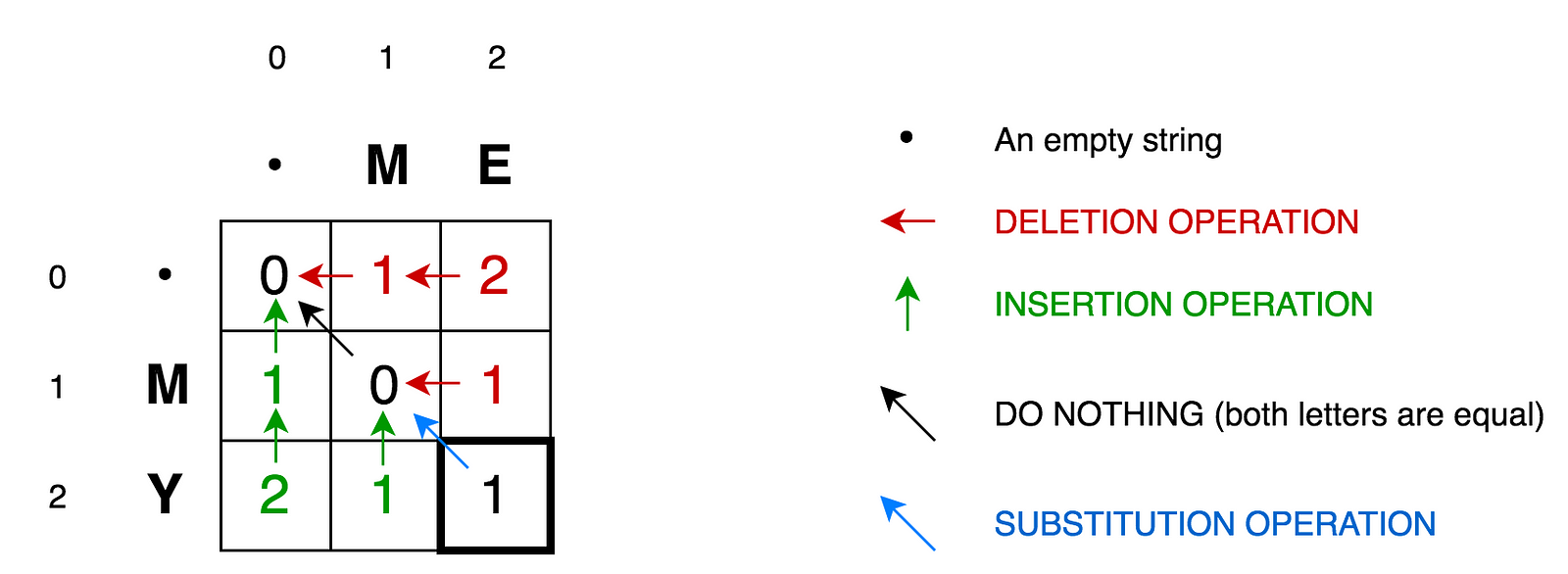
Để giải thích thêm điều này, hãy vẽ ma trận sau:
- Ô
(0:1)bao gồm con số đỏ 1. Có nghĩa là bạn cần 1 thao tác để chuyển đổiMthành một chuỗi trống. Thao tác đó là xoáM. Đó là lý do tại sao nó có màu đỏ. - Ô
(0:2)bao gồm con số đỏ 2. Có nghĩa là bạn cần 2 thao tác để chuyển đổiMEthành một chuỗi trống. Thao tác đó là xoáMvàE. - Ô
(1:0)bao gồm con số xanh 1. Có nghĩa là bạn cần 1 thao tác để chuyển đổi một chuỗi trống thànhM. Thao tác đó là thêmM. Đó là lý do tại sao nó màu xanh. - Ô
(2:0)bao gồm con số xanh 2. Có nghĩa là bạn cần 2 thao tác để chuyển đổi một chuỗi trống thànhMY. Thao tác đó là thêmMvàY. - Ô
(1:1)bao gồm số 0. Nó có nghĩa là không tốn gì để chuyển đổiMthànhM. - Ô
(1:2)bao gồm con số đỏ 1. Có nghĩa là bạn cần 1 thao tác để chuyển đổiMEthànhM. Thao tác đó là xoáE. - Và hơn thế nữa ...
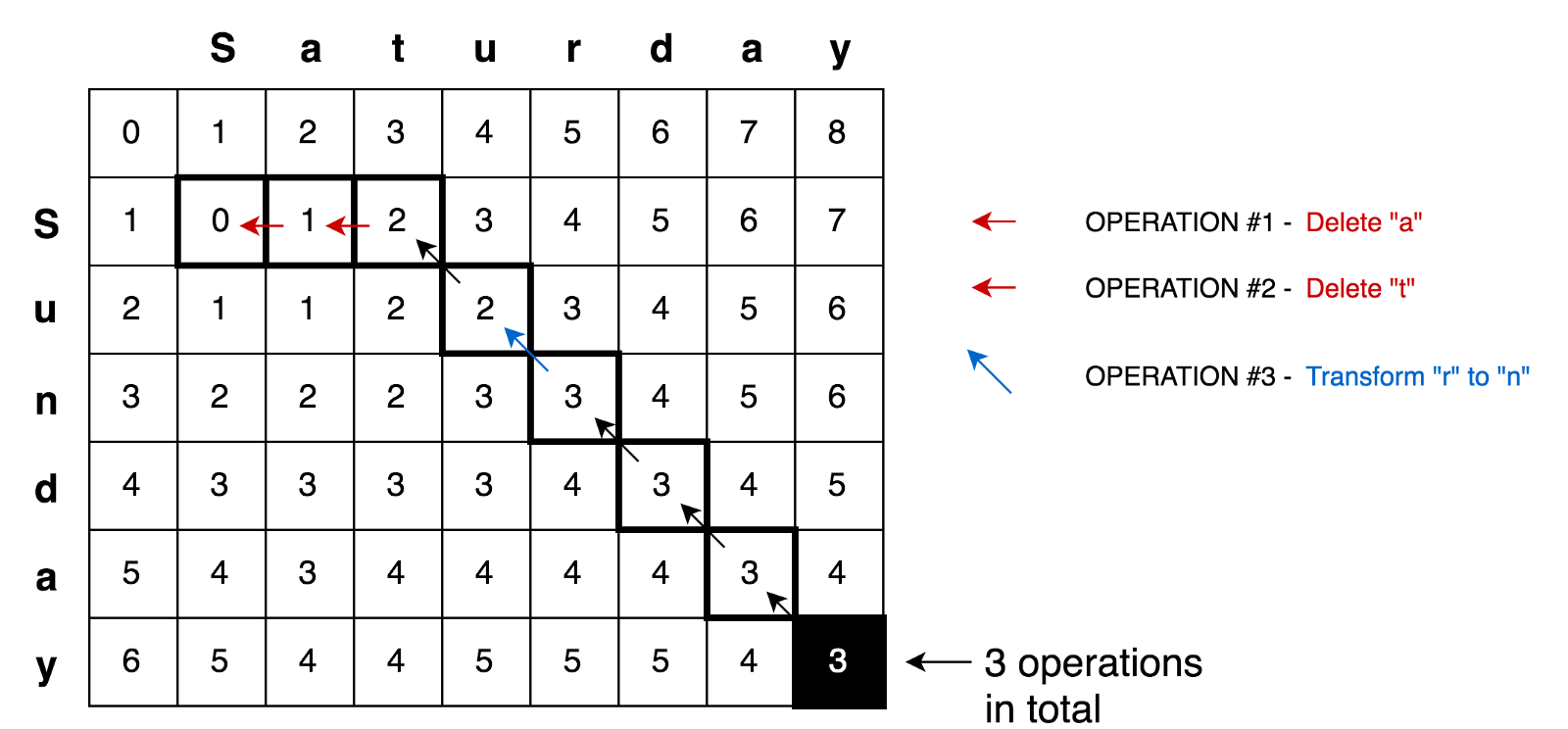
Điều này có vẻ dễ dàng đối với ma trận nhỏ như của chúng ta (nó chỉ là 3x3). Nhưng ở đây bạn có thể tìm thấy các khái niệm cơ bản có thể được áp dụng để tính toán tất cả các số đó cho ma trận lớn hơn (giả sử ma trận 9x7 cho phép biến đổi Saturday → Sunday).
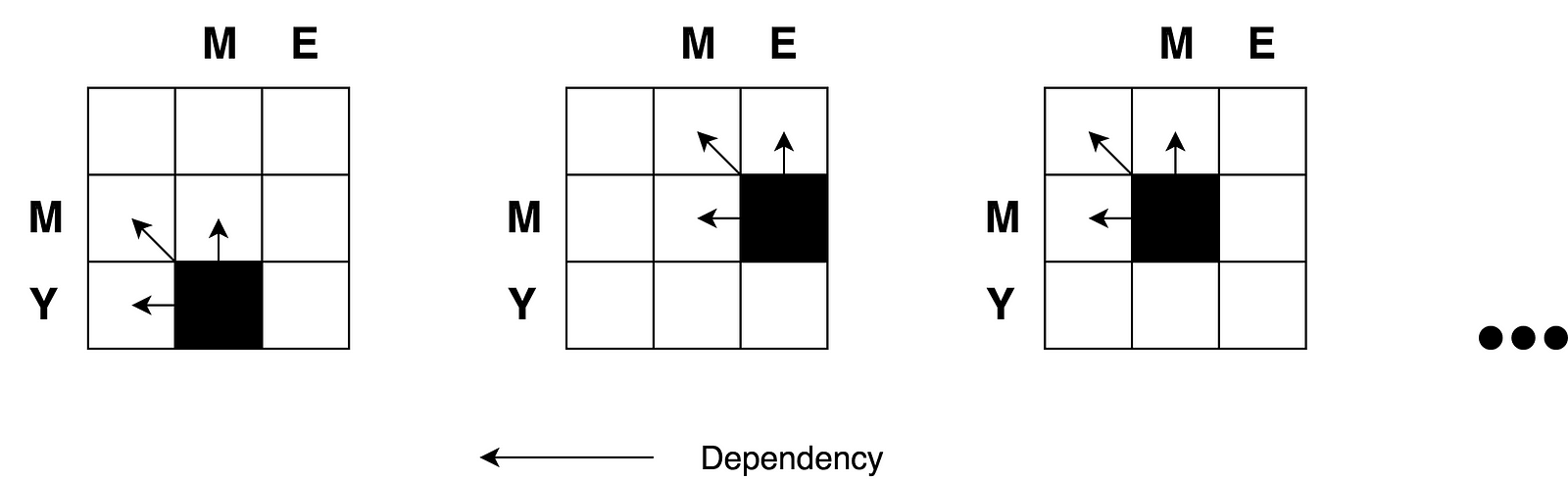
Theo công thức, bạn chỉ cần ba ô liền kề (i-1: j), (i-1: j-1), và (i: j-1) để tính số cho ô hiện tại (i: j). Tất cả những gì chúng ta cần làm là tìm số tối thiểu của ba ô đó và sau đó thêm 1 trong trường hợp nếu chúng ta có các chữ cái khác nhau trong hàng của i và cột của j.
Bạn có thể thấy rõ bản chất đệ quy của vấn đề.
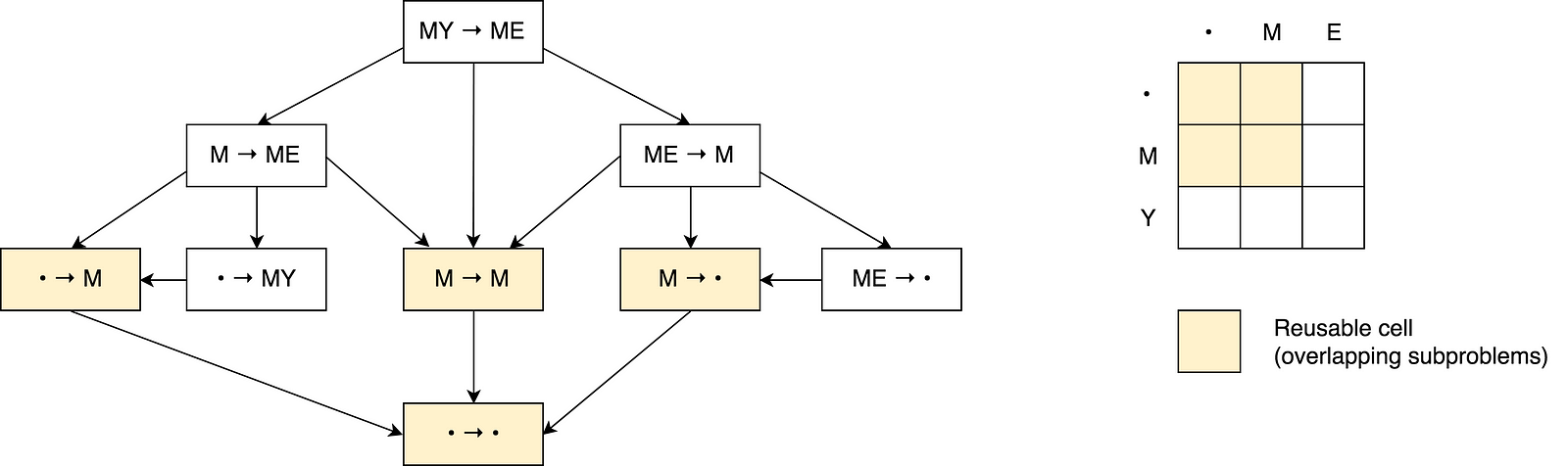
Hãy vẽ một biểu đồ giải quyết cho vấn đề này.
Bạn có thể thấy một số vấn đề phụ chồng chéo trên hình được đánh dấu bằng màu đỏ. Ngoài ra, không có cách nào để giảm số lượng hoạt động và làm cho nó ít hơn tối thiểu ba ô liền kề đó từ công thức.
Ngoài ra, bạn có thể nhận thấy rằng mỗi số ô trong ma trận đang được tính toán dựa trên những ô trước đó. Do đó, kỹ thuật lập bảng (lấp đầy bộ nhớ cache theo hướng từ dưới lên) đang được áp dụng ở đây.
Áp dụng nguyên tắc này hơn nữa, chúng tôi có thể giải quyết các trường hợp phức tạp hơn như chuyển đổi Saturday → Sunday.