看动画学算法系列之:后缀数组suffix array
[toc]
在之前的文章中,我们讲到了后缀树和它的一些特性。后缀树主要用来做模式匹配中,比如全文索引,寻找公共前缀等,非常的有用。同样的后缀数组和后缀树的作用非常类似,和后缀树相比,后缀数组更简单并且更加节省空间,今天我们将会详细介绍下后缀数组的特性和使用。
后缀数组和后缀树一样都是一个单词所有后缀的集合。只不过后缀数组把所有的后缀按照字母的顺序进行排序。
我们还是举之前的BANANA的例子,我们给这个单词一个加上一个后缀 $ , 假设 $ 按字母表排序是排在最上面的。那么我们的所有后缀如下图所示:
按照字母顺序排序之后生成的后缀数组如下:
先按首字母排序,如果首字母相同则第二个,以此类推。
构造后缀数组一般有两种方法:倍增算法和DC3算法。
这里我们详细的介绍一下怎么使用倍增算法来构建后缀数组。
回到我们上面提到的初始化状态和排序完成状态的两张图。
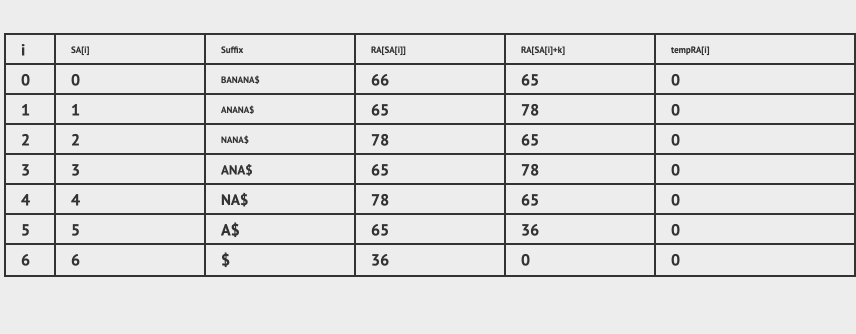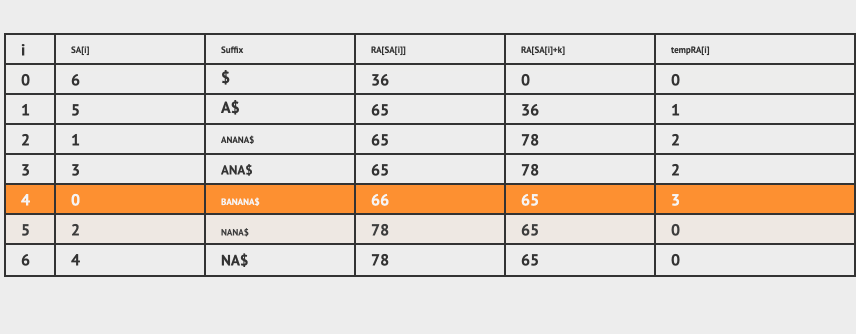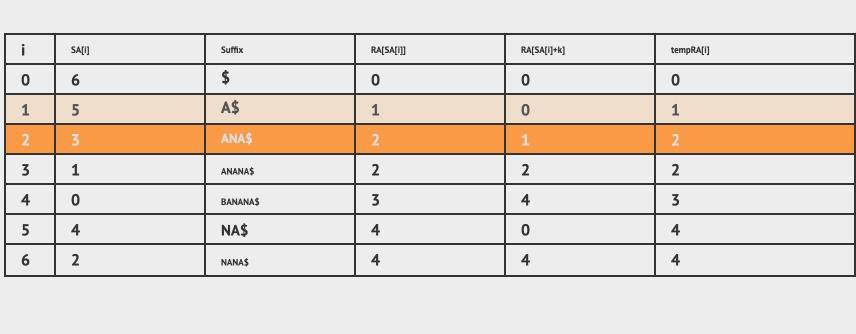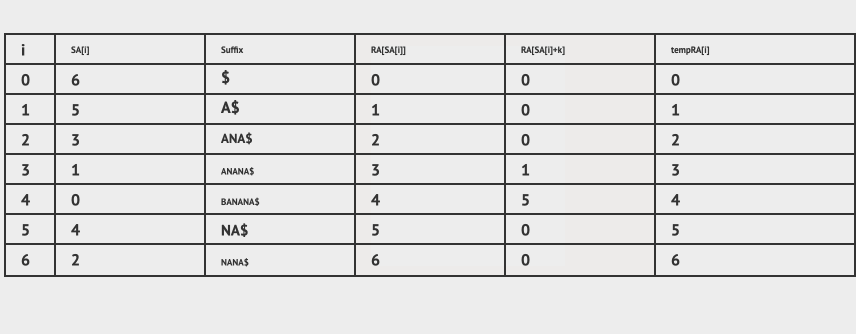
先介绍初始状态的图,图中我们定义了几个变量,分别是i,SA[i],Suffix, RA[SA[i]],RA[SA[i]+k],tempRA[i]。
其中SA[i]就是排序之后的后缀数组,也就是我们要的结果。SA[i] 的值是和Suffix一一对应的,表示从位置开始的后缀。
最开始的时候,因为还没有排序,我们将所有的后缀依次存放到SA[i]中,也就是SA[0] 中存放 0 开始的后缀也就是 BANANA$, SA[1] 中存放 1开始的后缀也就是 ANANA$,直到SA[6] 中存放 6 开始的后缀也就是 $。
RA[SA[i]] 表示的是 以 SA[i] 开始的后缀在排序后数组也就是SA中的排名,如果SA[i] = 0 , 对应的后缀是 BANANA$, 它在SA中的最终排名应该是 4 。也就是说在最终情况下 i = 4 , RA[SA[4]] = 4。
RA[SA[i] + k ] 是一个倍增辅助数组,其中k从1开始,每排过一轮之后,k = k * 2 。
我们的排序流程最终目标就是让 RA[SA[i]] = i ,下面看下怎么进行排序。
首先初始化 RA[SA[i]] 和 RA[SA[i] + k] ,第一轮的时候k=1, 我们取Suffix的首字母的ASCII值填充到RA[SA[i]] 和 RA[SA[i] + k] 中,超出数组范围部分我们置位 0, 于是得到下面的初始化图:
第二步,先按照RA[SA[i]] 进行排序,如果相同的话 再按照 RA[SA[i] + k] 进行排序,得到下面的图:
第三步,设置tempRA[i] 的值,从 0 开始, 比较第一次排序之后的 RA[SA[i]] 和 RA[SA[i] + k] 和上一条数据有没有变化,有就+1 , 否则保持不变。
比如第一行数据是 36,0 ,我们设置tempRA[0] =0 。
第二行数据是 65,36, 和前面一条数据不同,我们设置tempRA[1] =1 。
第三行数据是 65,78, 和前面一条数据不同,我们设置tempRA[2] =2 。
第四行数据是 65,78,和前面一条数据一样,我们设置tempRA[3] =2 。
最后我们得到tempRA数组的值为[0,1,2,2,3,4,4]。
得到tempRA数组之后,我们将tempRA的值拷贝给RA[SA[i]],然后将K * 2 ,重新计算 RA[SA[i]+2] 的值,得到下面的图:
接着将RA[SA[i]] 和 RA[SA[i]+2] 进行排序,按照上面的规则再次设置tempRA数组的值。
然后一直重复下去,直到RA[SA[i]] = i 。
我们看一个动画:
考虑下给定某个字符串,如何在后缀数组中找到一这个字符串开头的后缀呢?
其实很简单,因为后缀数组已经是按照字符的顺序进行排序了。我们想查找以某个字符串开头的所有后缀的话,可以在后缀数组中分别找到首次匹配的位置,然后找到最后匹配的位置,那么这两个位置中间的所有元素都是我们要找到的值。
还是上面的BANANA$,假如我们想找到以NA开头的字符串。
看下怎么查找:
基本流程就是使用二分法,先找到最小的匹配值也就是i=5, 然后再找到最小的匹配值也就是i=6。然后5和6之间的元素就是要查找的值。
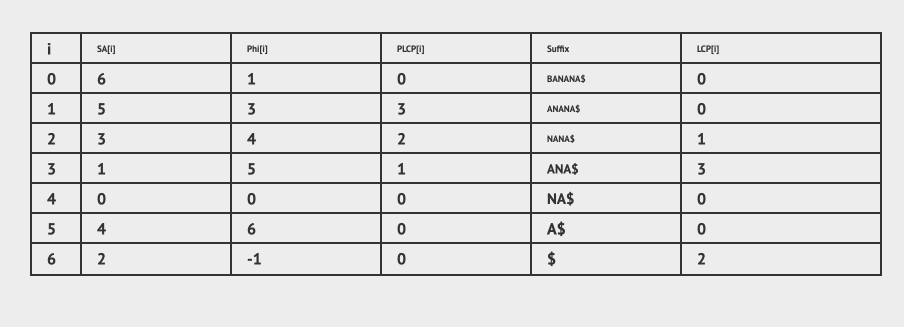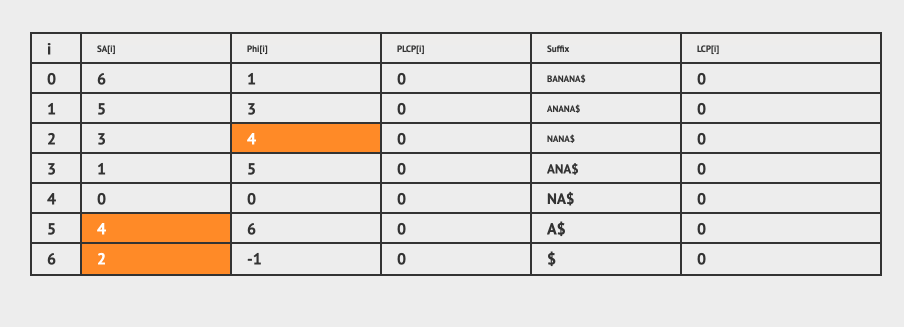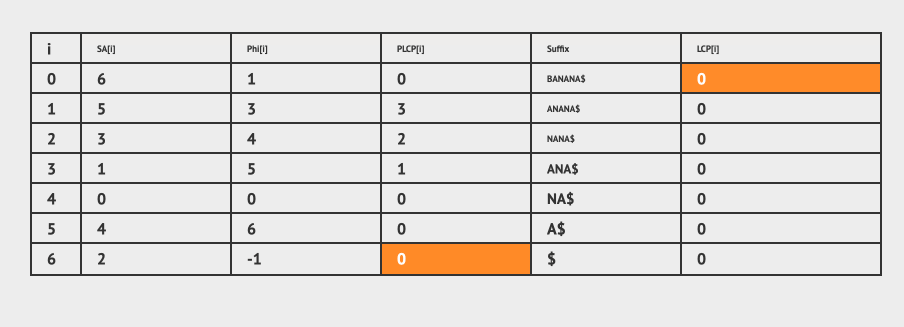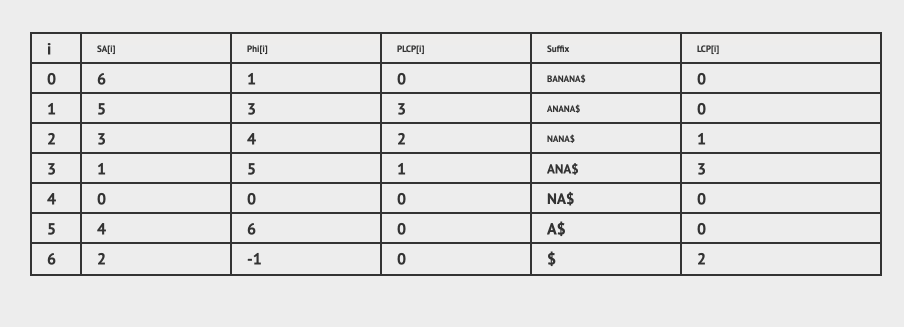
LCP的全称是最长公共前缀。我们看下BANANA的LCP定义:
从图上我们可以看出,LCP就是根据创建出的后缀数组得出来的,就是SA数组中当前位置代表的字符串和当前位置前面的一个位置代表的字符串的公共前缀。
举个例子,SA[2] = 3 , 3 代表的是字符串 ANA$, 它前面位置的值是SA[1] = 5 , 5 代表的字符串是 A$, 这两个字符串的公共前缀是A,所以相应的 LCP[2] = 1 。
那么怎么去创建这个LCP呢?
这里介绍一个算法叫做 Permuted LCP 。
这个算法引入了一个叫做PLCP的数组,这个数组实际上就是将LCP按照原字符串的顺序进行排序,如下图所示:
很显然,我们有下面的特性: LCP[i] = PLCP[SA[i]]
那么怎么创建PLCP呢?
考虑一下PLCP[0], 因为是按照原字符串的顺序进行排列的,所以PLCP[0]对应的是BANANA$ 这个字符串和后缀数组SA中排在它前面的字符串ANANA$ 的公共前缀。
BANANA$ 在原字符串中出现的位置是0,也就是PLCP中的i。我们只需要找到ANANA$ 在原字符串中的位置k即可,然后通过比较T[i + L] == T[k + L] 从而找出公共前缀的长度L。
为此,我们创建一个辅助数组Phi,让Phi[SA[i]] = SA[i-1],那么可以得出 Phi[i] = k, 这样我们就找到了i和k关系。
对应的代码如下:
void computeLCP() {
int i, L;
Phi[SA[0]] = -1; // default value
for (i = 1; i < n; i++) // compute Phi in O(n)
Phi[SA[i]] = SA[i-1]; // remember which suffix is behind this suffix
for (i = L = 0; i < n; i++) { // compute Permuted LCP in O(n)
if (Phi[i] == -1) { PLCP[i] = 0; continue; } // special case
while (i + L < T.length && Phi[i] + L < T.length && T[i + L] == T[Phi[i] + L]) L++; // L will be increased max n times
PLCP[i] = L;
L = Math.max(L-1, 0); // L will be decreased max n times
}
for (i = 1; i < n; i++) // compute LCP in O(n)
LCP[i] = PLCP[SA[i]]; // put the permuted LCP back to the correct position
}我们看下动画表示:
后缀数组和后缀树的功能基本上类似,但是后组数组易于理解,编程和调试,在信息学竞赛中用到的比较多。而后缀树占用的空间比较多,我们在使用的时候可以根据需要进行选择。
本文已收录于 www.flydean.com
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!