看动画学算法之:排序-归并排序
归并排序简称Merge sort是一种递归思想的排序算法。这个算法的思路就是将要排序的数组分成很多小的部分,直到这些小的部分都是已排序的数组为止(只有一个元素的数组)。
然后将这些排序过的数组两两合并起来,组成一个更大一点的数组。接着将这些大一点的合并过的数组再继续合并,直到排序完整个数组为止。
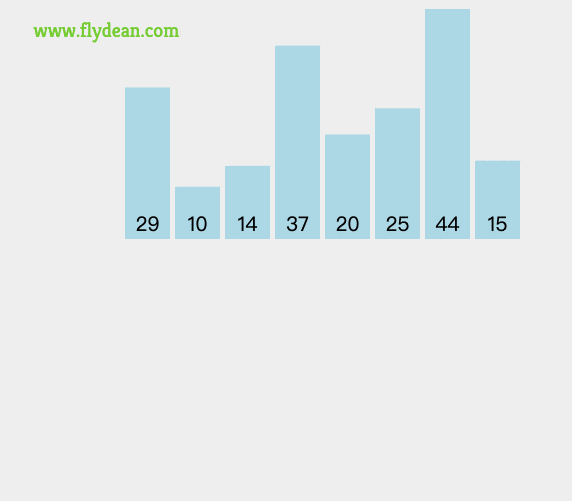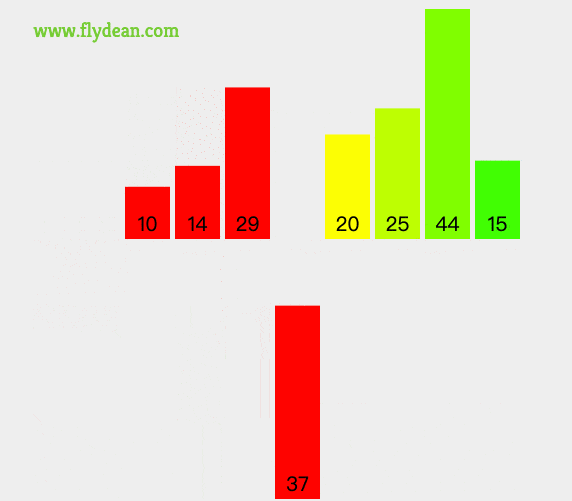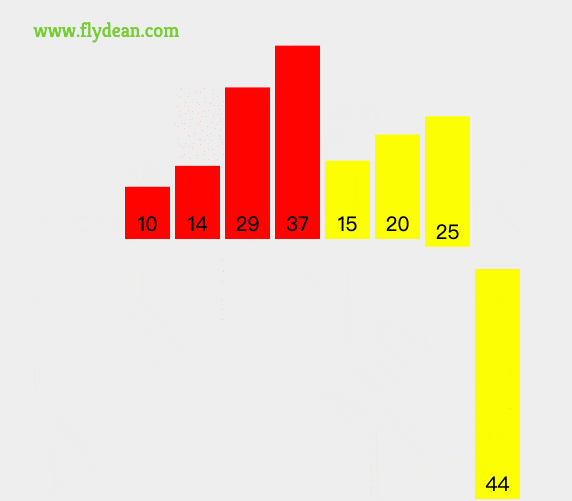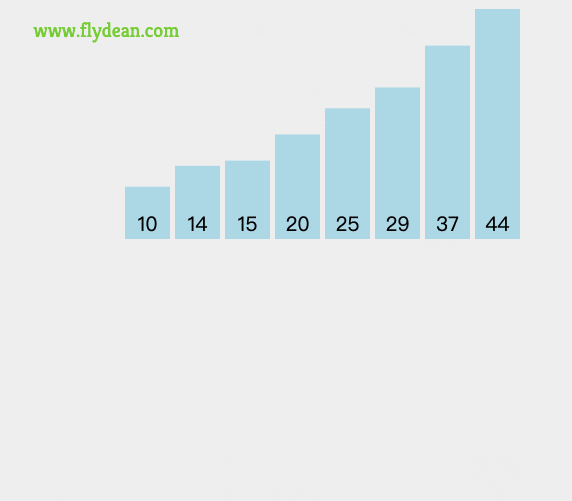
假如我们有一个数组:29,10,14,37,20,25,44,15,怎么对它进行归并排序呢?
先看一个动画:
我们来详细分析一下上面例子的运行过程:
首先将数组分为两部分,[29,10,14,37]和[20,25,44,15]。
[29,10,14,37]又分成两部分[29,10]和[14,37]。
[29,10]又被分成两部分[29]和[10],然后对[29]和[10]进行归并排序生成[10,29]。
同样的对[14,37]进行归并排序得到[14,37]。
将[10,29]和[14,37]再次进行归并排序得到[10,14,29,37],以此类推,得到最后的结果。
归并排序主要使用了分而治之的思想。将一个大的数组分成很多很多个已经排序好的小数组,然后再对小数组进行合并。
这个Divide的过程可以使用递归算法,因为不管是大数组还是小数组他们的divide逻辑是一样的。
而我们真正做排序的逻辑部分是在合并这一块。
先看一下最核心的merge部分:
/**
*合并两部分已排序好的数组
* @param array 待合并的数组
* @param low 数组第一部分的起点
* @param mid 数组第一部分的终点,也是第二部分的起点-1
* @param high 数组第二部分的终点
*/
private void merge(int[] array, int low, int mid, int high) {
// 要排序的数组长度
int length = high-low+1;
// 我们需要一个额外的数组存储排序过后的结果
int[] temp= new int[length];
//分成左右两个数组
int left = low, right = mid+1, tempIdx = 0;
//合并数组
while (left <= mid && right <= high) {
temp[tempIdx++] = (array[left] <= array[right]) ? array[left++] : array[right++];
}
//一个数组合并完了,剩下的一个继续合并
while (left <= mid) temp[tempIdx++] = array[left++];
while (right <= high) temp[tempIdx++] = array[right++];
//将排序过后的数组拷贝回原数组
for (int k = 0; k < length; k++) array[low+k] = temp[k];
}大家需要注意的是,我们的元素是存在原始数组里面的,方法的第一个参数就是原始数组。
后面的三个参数是数组中需要归并排序的index。三个index将数组划分成了两部分:array[low to mid], array[mid+1 to high]。
merge的逻辑就是对这两个数组进行合并。
因为我们的数组本身是存放有原始的,所以要想进行归并排序,我们需要借助一个额外的数组空间int[] temp。
通过比较array[low to mid], array[mid+1 to high]中的元素大小,一个个将元素插入到int[] temp中,最后将排序过后的数组拷贝回原数组,merge完成。
然后我们再看一下divide的部分,divide部分实际上就是递归调用,在递归的最后,我们需要调用merge方法即可:
public void doMergeSort(int[] array, int low, int high){
// 要排序的数组 array[low..high]
//使用二分法进行递归,当low的值大于或者等于high的值的时候,就停止递归
if (low < high) {
//获取中间值的index
int mid = (low+high) / 2;
//递归前面一半
doMergeSort(array, low , mid );
//递归后面一半
doMergeSort(array, mid+1, high);
//递归完毕,将排序过后的数组的两部分合并
merge(array, low, mid, high);
log.info("merge之后的数组:{}",array);
}
}array是原数组,low和high标记出了要递归排序的数组起始位置。
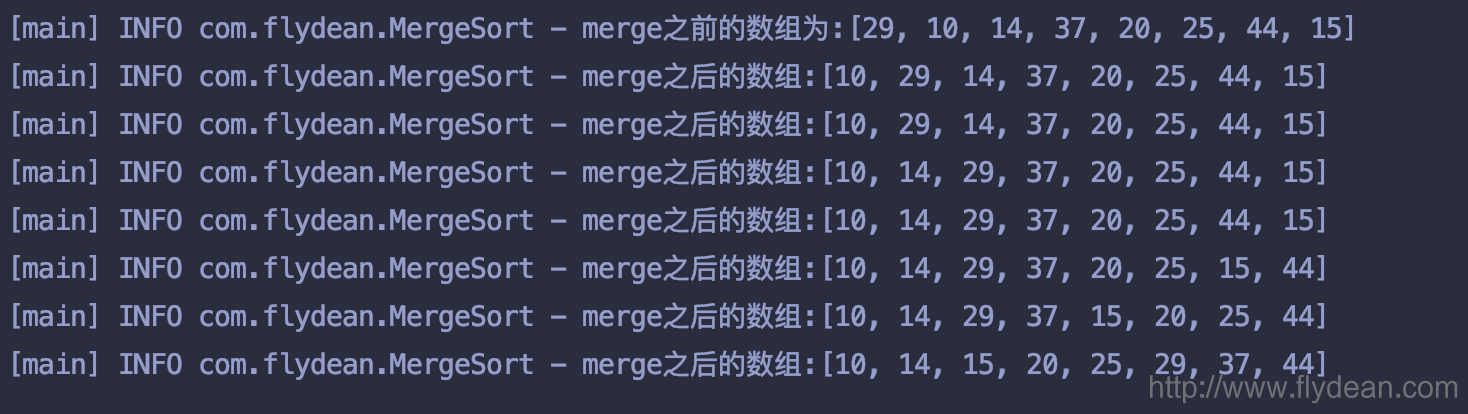
运行下上面的结果:
可以看到输出结果和我们动画展示的结果是一致的。
我们看下归并排序的时间复杂度是怎么样的。
首先看merge方法,merge方法实际是遍历了两个数组,所以merge方法的时间复杂度是O(N)。
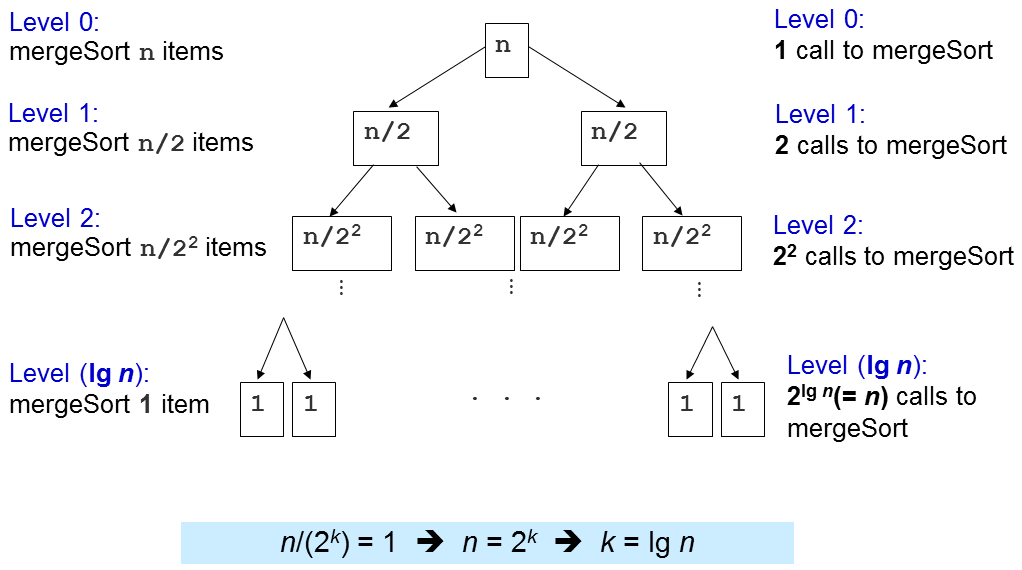
再看一下divide方法:
divide方法将排序分成了logN层,每层都可以看做是对N个元素的合并排序,因此每层的时间复杂度是O(N)。
加起来,总的时间复杂度就是O(N logN)。
本文的代码地址:
本文已收录于 www.flydean.com
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!