s0051_n_queens

51. N-Queens

Hard

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Example 1:

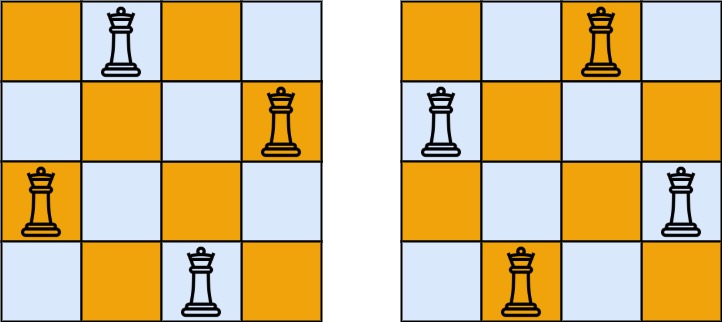
Input: n = 4

Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]

Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:

Input: n = 1

Output: [["Q"]]

Constraints:

• 1 <= n <= 9

To solve the "N-Queens" problem in Swift with the Solution class, follow these steps:

1. Define a method solveNQueens in the Solution class that takes an integer n as input and returns a list of lists of strings.
2. Initialize a board represented as a 2D character array of size n x n. Initialize all cells to '.', indicating an empty space.
3. Define a recursive backtracking function backtrack to explore all possible configurations of queens on the board.
4. In the backtrack function:
   • Base case: If the current row index row is equal to n, it means we have successfully placed n queens on the board. Add the current board configuration to the result.
   • Iterate through each column index col from 0 to n - 1:
     • Check if it's safe to place a queen at position (row, col) by calling a helper function isSafe.
     • If it's safe, place a queen at position (row, col) on the board, mark it as 'Q'.
     • Recur to the next row by calling backtrack(row + 1).
     • Backtrack: After exploring all possibilities, remove the queen from position (row, col) by marking it as '.'.
5. In the solveNQueens method, initialize an empty list result to store the solutions.
6. Call the backtrack function with initial parameters 0 for the row index.
7. Return the result list containing all distinct solutions.

Here's the implementation of the solveNQueens method in Swift:

public class Solution {
    public func solveNQueens(_ n: Int) -> [[String]] {
        var pos = [Bool](repeating: false, count: n + 2 * n - 1 + 2 * n - 1)
        var pos2 = [Int](repeating: 0, count: n)
        var ans = \[\[String]]()
        helper(n, 0, &pos, &pos2, &ans)
        return ans
    }

    private func helper(_ n: Int, _ row: Int, _ pos: inout [Bool], _ pos2: inout [Int], _ ans: inout [[String]]) {
        if row == n {
            construct(n, pos2, &ans)
            return
        }
        for i in 0..<n {
            let index = n + 2 * n - 1 + n - 1 + i - row
            if pos[i] || pos[n + i + row] || pos[index] {
                continue
            }
            pos[i] = true
            pos[n + i + row] = true
            pos[index] = true
            pos2[row] = i
            helper(n, row + 1, &pos, &pos2, &ans)
            pos[i] = false
            pos[n + i + row] = false
            pos[index] = false
        }
    }

    private func construct(_ n: Int, _ pos: [Int], _ ans: inout [[String]]) {
        var sol = [String]()
        for r in 0..<n {
            var queenRow = [Character](repeating: ".", count: n)
            queenRow[pos[r]] = "Q"
            sol.append(String(queenRow))
        }
        ans.append(sol)
    }
}

This implementation efficiently finds all distinct solutions to the N-Queens problem using backtracking.