Solving P1 and P3 formulations from the paper: Calik H, Tansel BC (2013) Double bound method for solving the p-center location problem. Comput Oper Res 40:2991–2999
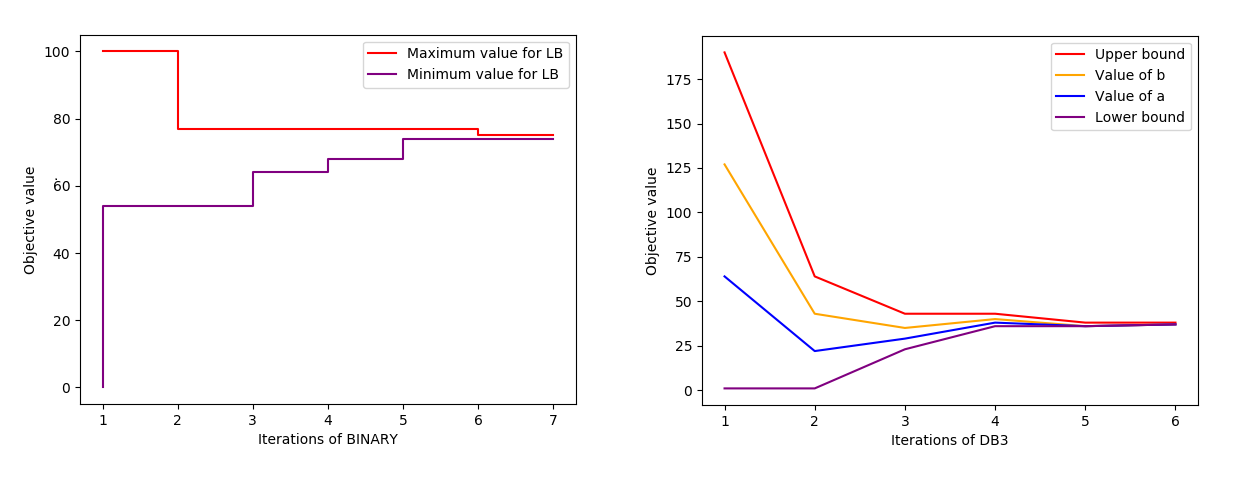
The BINARY and DB3 algorithms from the same paper have been implemented in order to solve P3 efficiently.
julia> Pkg.add("ArgParse")
julia> Pkg.add("Cbc")
julia> Pkg.add("GLPKMathProgInterface")
julia> Pkg.add("JuMP")General command syntax:
$ julia solve.jl <path-to-instance> <form> [--solver SOLVER]Argument "form" must be either "p1", "p3", "p3-binary" or "p3-db3". Argument "solver" can be either "cbc" or "glpk" (default value is "cbc").
The script will create a folder "results" in current directory and write the results for given formulation, instance and solver in a txt file.
$ julia solve.jl path-to-instance p1$ julia solve.jl path-to-instance p3-db3