1008.md

title	description	keywords
1008. 前序遍历构造二叉搜索树	LeetCode 1008. 前序遍历构造二叉搜索树题解，Construct Binary Search Tree from Preorder Traversal，包含解题思路、复杂度分析以及完整的 JavaScript 代码实现。	LeetCode 1008. 前序遍历构造二叉搜索树 前序遍历构造二叉搜索树 Construct Binary Search Tree from Preorder Traversal 解题思路 栈 树 二叉搜索树 数组 二叉树 单调栈

1008. 前序遍历构造二叉搜索树

🟠 Medium  🔖  栈 树 二叉搜索树 数组 二叉树 单调栈  🔗 力扣 LeetCode

题目

Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree ), construct the tree and return its root.

It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.

A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.

A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.

Example 1:

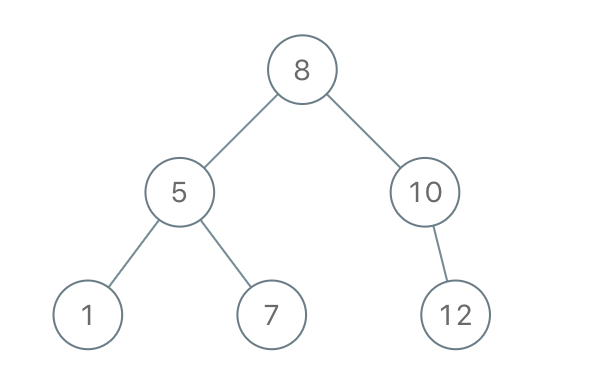
Input: preorder = [8,5,1,7,10,12]

Output: [8,5,10,1,7,null,12]

Example 2:

Input: preorder = [1,3]

Output: [1,null,3]

Constraints:

• 1 <= preorder.length <= 100
• 1 <= preorder[i] <= 1000
• All the values of preorder are unique.

题目大意

给定一个整数数组，它表示 BST(即 二叉搜索树 )的 先序遍历 ，构造树并返回其根。

保证 对于给定的测试用例，总是有可能找到具有给定需求的二叉搜索树。

二叉搜索树 是一棵二叉树，其中每个节点， Node.left 的任何后代的值 严格小于 Node.val , Node.right 的任何后代的值 严格大于 Node.val。

二叉树的 前序遍历 首先显示节点的值，然后遍历Node.left，最后遍历Node.right。

解题思路

构造二叉树，先找到根节点，再递归地构造左右子树。

本题中已知二叉搜索树的先序遍历，根节点就是数组的第一个元素。

只需要再找出左右子树分割的地方，就可以递归构造左右子树了。根据二叉搜索树的特点，左子树的所有值都小于根节点，所以只需遍历后续数组，找到第一个比根节点大的数值，即为右子树先序遍历的第一个元素。

代码

/**
 * @param {number[]} preorder
 * @return {TreeNode}
 */
var bstFromPreorder = function (preorder) {
	if (!preorder.length) return null;
	let root = new TreeNode(preorder[0]);
	let mid = 1;
	while (preorder[mid] < preorder[0]) {
		mid++;
	}
	root.left = bstFromPreorder(preorder.slice(1, mid));
	root.right = bstFromPreorder(preorder.slice(mid));
	return root;
};