树结构的重要性无容置疑,这是计算机世界的基础,毫不夸张的说,一个对树不了解的人实际上是很难被称之为开发者的,而由于其比数组,链表等线性结构更复杂,想真正理解需要不断重复,这里记录的就是我的一次重复的过程而已。
这里选择使用swift进行来实现,因为过程相当舒适,并且参考了swift-algorithm-club,对所有贡献者表示感谢
基本概念用一张图标示:

- 节点及构建
*为集中于基本概念的夯实而不分散注意力,所以当前会简单的规定节点值为特定类型,而用泛型
首先我们需要节点,而节点应该包含哪些信息呢?这是我们需要思考的,我想起码应该包含当前节点值,其父节点(树节点一般都是有且只有一个父节点的)和孩子们(这里也是使用最简单的数据来实现),故:
class Node {
var value: String
var children: [Node] = []
weak var parent: Node?
init(value: String) {
self.value = value
}
}我们有了节点了,下来就是添加孩子从而构成树,所以增加一个方法:
func add(child: Node) {
child.parent = self
self.children.append(child)
}添加操作中最重要的就是增加逻辑关系,即确定父子关系
如此,我们就可以初始化一个自己的树结构了,比如NBA结构树:
let nba = Node(value: "NBA")
let west = Node(value: "WestSec")
let east = Node(value: "EastSec")
nba.add(child: east)
nba.add(child: west)- 打印Print
为查看方便,重写一下CustomStringConvertible,如下:
extension Node: CustomStringConvertible {
var description: String {
var text = "\(value)"
/* 这里使用了map和递归,如果感到困惑的化,不妨使用
if !children.isEmpty {
text += " [<- "
for child in children {
if children.last?.value != child.value {
text += child.description + " -- "
} else {
text += child.description
}
}
text += " ->] "
}
*/
if(!children.isEmpty) {
text += " [<- " + children.map {
$0.description
}.joined(separator: " -- ") + " ->] "
}
return text
}
}这里使用了递归,暂时也不用分太多的精力,姑且只是当作一个专有的输出工具即可,在多加几个节点丰富一下我们的树以后,打印结果如下:
NBA [<- EastSec [<- CEltics -- BULLs -- NETs ->] -- WestSec [<- LAKERs -- ROCKETs -- Spurs ->] ->] 虽然算不上很友好,但意思对了,综上,我们再把泛型加上,就得到了一个简单的树:
class Node<T> {
var value: T
weak var parent: Node?
var children: [Node] = []
init(value: T) {
self.value = value
}
func add(child: Node) {
children.append(child)
child.parent = self
}
}
// 增加一个search方法
extension Node where T: Equatable {
func search(value: T) -> Node? {
if value == self.value {
return self
}
for child in children {
if let found = child.search(value: value) {
return found
}
}
return nil
}
}
// ------ test ---------
let nba = Node(value: "NBA")
let west = Node(value: "WestSec")
let east = Node(value: "EastSec")
nba.add(child: east)
nba.add(child: west)
let lakers = Node(value: "LAKERs")
let rockets = Node(value: "ROCKETs")
let spurs = Node(value: "Spurs")
west.add(child: lakers)
west.add(child: rockets)
west.add(child: spurs)
let nets = Node(value: "NETs")
let celtics = Node(value: "CEltics")
let bull = Node(value: "BULLs")
east.add(child: celtics)
east.add(child: bull)
east.add(child: nets)
print(nba)我们从典型而简单的二叉树(binary tree)进行探讨,当每个节点最多有2个孩子的树,我们称之为二叉树(binary tree),分别称之为左右孩子(left/right child),当节点没有孩子时,仍就称之为叶子(leaf),这其中如果最后一层全部是叶子时就是满二叉树(节点数 = 2的层数次幂数 - 1)
比如对于一个多项式(5 * (a - 10)) + (-4 * (3 / b)), 借助二叉树可存储为:
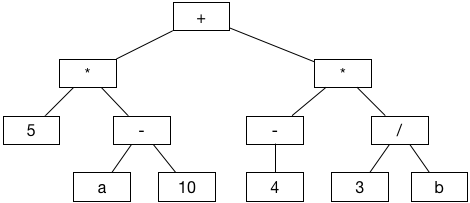
当我们使用中序遍历(inorder Traversal)时,就能还原上述多项式的计算逻辑,当然还有前序遍历(preorder traversal)和后序遍历(postorder traversal)其他遍历方式,可以看出前中后指的就是对任意子树中根处理的前中后,不同情况下根据逻辑选取不用的遍历方式
二叉树的遍历有递归(Recursive)和迭代(Iterative)2中方式,其中递归一旦理解了就很简单明了,但很反直觉,而迭代更容易理解一些,先说递归:
/**
A
/ \
B C
\ / \
D E F
*/
// 前序 & 递归
private func preOder(root: BiTNode?) {
guard let curr = root else {
return
}
print(curr.value)
preOder(root: curr.letfChild)
preOder(root: curr.rightChild)
}
// 前序 & 迭代 + stack
private func preOrder(root: BiTNode?) {
var arr: [BiTNode] = []
var curr = root
while true {
if curr != nil {
print(" push--> " + curr!.value)
arr.append(curr!)
curr = curr!.letfChild
}else {
if arr.count == 0 {
break;
}
let last = arr.last
print(" pop--> " + (last!.value))
arr.removeLast()
curr = last!.rightChild
}
}
}其递归流程如图
一个递归单元在干什么以及何时退出。而递归的核心问题在于2点:使用的数据结构 以及 如何从左子树切换到右子树,这里使用了栈